matlab离散系统 响应,MATLAB离散系统响应分析与仿真技巧

你有没有想过，那些看似复杂的电子设备，其实背后都隐藏着一个个神奇的数学世界？在这个世界里，MATLAB离散系统响应就像是一把钥匙，能解锁那些隐藏在电路中的秘密。今天，就让我带你一起探索MATLAB离散系统响应的奇妙之旅吧！

MATLAB：你的数字信号处理好帮手

MATLAB，这个在工程和科学领域大名鼎鼎的软件，它不仅可以帮助我们解决复杂的数学问题，还能让我们轻松地研究离散系统响应。想象你手中拿着一个神秘的电路，MATLAB就像一位高明的侦探，帮你一步步揭开它的神秘面纱。

离散系统：电路的数学语言

离散系统，顾名思义，就是那些在时间上不连续的系统。在我们的生活中，有很多离散系统的例子，比如数字信号处理、通信系统、控制系统等。而离散系统响应，就是描述这些系统在输入信号作用下的输出信号。

MATLAB离散系统响应：从零开始

想要研究离散系统响应，首先你得有一个离散系统。在MATLAB中，我们可以用差分方程来描述离散系统。比如，一个简单的离散系统可以用以下差分方程来表示：

y(n) - 1.6y(n-1) - 1.28y(n-2) = 0.5x(n) - 0.1x(n-1)

这个方程告诉我们，系统的输出y(n)与输入x(n)以及过去的输出值有关。那么，如何用MATLAB来求解这个方程呢？

首先，我们需要定义系统的差分方程。在MATLAB中，我们可以使用`filter`函数来求解差分方程。下面是一个简单的例子：

```matlab

a = [1 -1.6 -1.28];

b = [0.5 -0.1];

x = [2 1 3 4 5 6]; % 输入信号

y = filter(b, a, x); % 求解差分方程

运行这段代码后，我们就可以得到系统的输出信号y。

MATLAB离散系统响应：时域分析

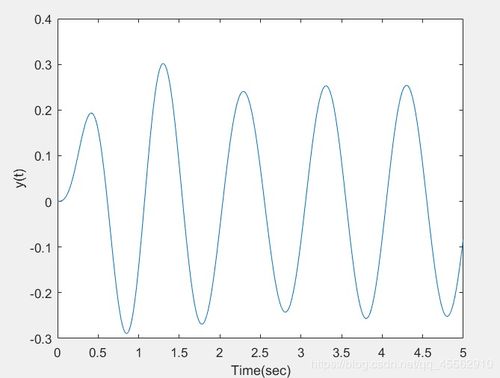
得到系统的输出信号后，我们就可以对它进行时域分析了。在MATLAB中，我们可以使用`plot`函数来绘制系统的输出信号波形。

```matlab

t = 0:length(y)-1;

plot(t, y);

xlabel('时间');

ylabel('输出');

title('系统输出信号波形');

通过观察波形，我们可以了解系统的动态特性，比如上升时间、下降时间、稳定时间等。

MATLAB离散系统响应：频域分析

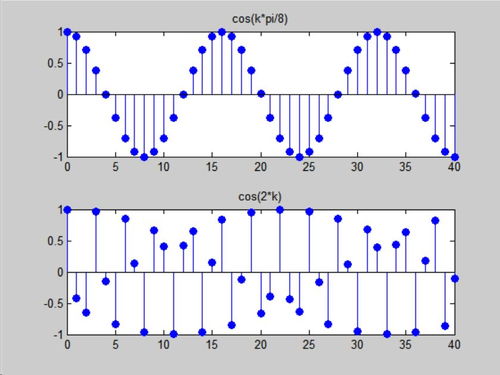
除了时域分析，我们还可以对离散系统响应进行频域分析。在MATLAB中，我们可以使用`fft`函数来计算信号的频谱。

```matlab

Y = fft(y);

f = (0:length(Y)-1)(Fs/length(Y));

plot(f, abs(Y));

xlabel('频率');

ylabel('幅度');

title('系统输出信号频谱');

通过观察频谱，我们可以了解系统的频率特性，比如截止频率、带宽等。

MATLAB离散系统响应：稳定性分析

稳定性是离散系统的一个重要特性。在MATLAB中，我们可以使用`zplane`函数来绘制系统的零极点图，从而判断系统的稳定性。

```matlab

zplane(b, a);

如果所有的极点都位于单位圆内部，那么系统是稳定的。否则，系统是不稳定的。

MATLAB离散系统响应：应用实例

MATLAB离散系统响应在各个领域都有广泛的应用。比如，在通信系统中，我们可以使用MATLAB来设计滤波器，从而提高信号的传输质量；在控制系统中，我们可以使用MATLAB来设计控制器，从而实现对系统的精确控制。

MATLAB离散系统响应就像是一把神奇的钥匙，能帮助我们解锁电路中的秘密。通过MATLAB，我们可以轻松地研究离散系统响应，从而更好地理解电路的奥秘。让我们一起走进MATLAB的数字信号处理世界，探索那些隐藏在电路中的奇妙之旅吧！