matlab 连续系统,Matlab连续系统建模与仿真技术解析

想象你正站在一个充满无限可能的数字世界中，手中握着一把开启智慧之门的钥匙——那就是MATLAB。今天，我们就来聊聊这个强大的工具如何将连续系统的复杂世界，转化为我们触手可及的数字模型。

MATLAB：数字世界的魔法师

MATLAB，一个听起来就充满科技感的名字，它不仅仅是一个软件，更像是连接现实与虚拟的桥梁。在这个桥梁上，我们可以用MATLAB将连续系统的各种特性，如速度、加速度、位移等，转化为计算机可以处理的数字信号。

连续系统：现实世界的缩影

在现实世界中，许多物理现象都可以用连续系统来描述。比如，一辆汽车在行驶过程中，其速度、加速度和位移都是连续变化的。这些连续变化的物理量，在MATLAB的世界里，如何被赋予数字生命呢？

离散化：从连续到数字的跨越

要将连续系统转化为数字模型，首先需要进行离散化处理。简单来说，就是将连续的物理量，按照一定的时间间隔，转化为离散的数值。这个过程，就像是将一条连续的河流，分割成一段段的小溪。

在MATLAB中，我们可以通过以下几种方法实现离散化：

1. 欧拉法：这是一种最简单的离散化方法，它假设在每一个时间间隔内，系统的状态变化是线性的。

2. 梯形法：这种方法比欧拉法更精确，它假设在每一个时间间隔内，系统的状态变化是梯形的。

3. 辛普森法：这是一种更精确的离散化方法，它假设在每一个时间间隔内，系统的状态变化是抛物线的。

MATLAB中的连续系统

在MATLAB中，我们可以使用多种工具来处理连续系统。以下是一些常用的工具：

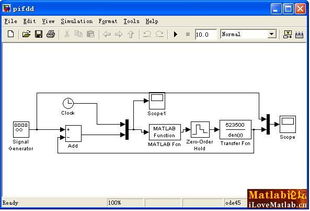
1. Simulink：Simulink是一个基于MATLAB的仿真环境，它允许我们创建和模拟复杂的系统模型。

2. 控制系统工具箱：这个工具箱提供了丰富的控制系统建模、分析和设计功能。

3. 信号处理工具箱：这个工具箱提供了信号处理的各种算法，可以帮助我们处理连续系统的信号。

MATLAB中的连续系统实例

让我们以一个简单的例子来说明如何在MATLAB中处理连续系统。假设我们有一个质量-弹簧-阻尼系统，其微分方程为：

m d^2x/dt^2 + c dx/dt + k x = F(t)

其中，m是质量，c是阻尼系数，k是弹簧系数，F(t)是外力。

在MATLAB中，我们可以使用以下代码来模拟这个系统：

```matlab

% 定义参数

m = 1;

c = 0.5;

k = 1;

F = @(t) sin(2pit);

% 定义时间序列

t = 0:0.01:10;

% 求解微分方程

x = ode45(@(t,x) [x(2); (F(t) - cx(2) - kx(1))/m], t, [0; 0]);

% 绘制结果

plot(t, x(:,1));

xlabel('时间');

ylabel('位移');

title('质量-弹簧-阻尼系统');

这段代码使用了MATLAB的ode45函数来求解微分方程，并绘制了位移随时间的变化曲线。

MATLAB是一个强大的工具，它可以帮助我们处理连续系统的各种问题。通过离散化、仿真和数据分析，我们可以更好地理解连续系统的行为，并将其应用于实际工程中。在这个数字世界中，MATLAB就像一位魔法师，将现实与虚拟完美结合。