7723游戏盒安卓版

在计算机科学和算法领域，二叉树是一种常见的树形数据结构。它由节点组成，每个节点最多有两个子节点，分别称为左子节点和右子节点。二叉树在许多应用中都有广泛的应用，如排序、搜索、路径查找等。本文将介绍一种基于二叉树的趣味游戏——二叉树着色游戏，并探讨其背后的算法和策略。

游戏规则

二叉树着色游戏是一种两人对弈游戏，游戏的目标是着色尽可能多的节点。游戏开始时，两位玩家分别选择一个奇数个节点的二叉树，并从1到n中选取两个不同的值x和y（1 游戏进行时，两位玩家轮流进行操作。每个玩家可以选择一个已经被自己染色的节点，然后将其一个未着色的邻节点（包括左右子节点或父节点）染上自己的颜色。如果当前玩家无法找到可以染色的节点，则其回合将被跳过。游戏在两位玩家都无法找到可染色节点时结束。

算法分析

节点数量分析：由于n为奇数，所以二叉树中节点总数为n。为了确保二号玩家能够着色更多的节点，他需要选择一个值y，使得y所在的子树节点数尽可能多。

染色策略：在游戏过程中，二号玩家需要根据当前树的结构和已着色节点的分布，选择合适的节点进行染色，以最大化自己的着色节点数。

动态规划：可以使用动态规划的方法来分析二号玩家在不同情况下的最优策略。通过计算每个节点在游戏结束时的最大着色节点数，可以确定二号玩家是否能够赢得游戏。

示例分析

以下是一个示例，说明如何使用动态规划的方法分析二号玩家是否能够赢得游戏：

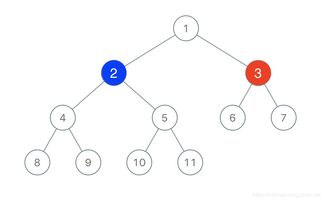
假设输入的二叉树为：

1

/ \\

2 3

/ \\ / \\

4 5 6 7

其中，n=7，x=3。二号玩家可以选择值y=2，并给值为2的节点染上蓝色。以下是动态规划的过程：

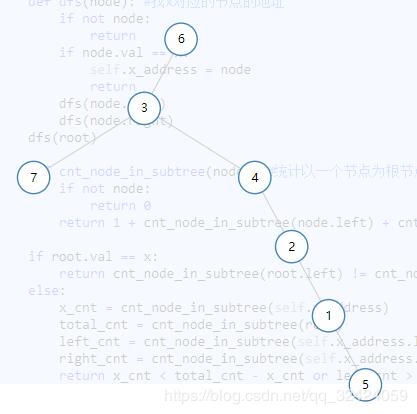
计算节点1的最大着色节点数：由于节点1没有子节点，所以其最大着色节点数为0。

计算节点2的最大着色节点数：节点2有两个子节点，分别为节点4和节点5。由于节点4和节点5都未被染色，所以节点2的最大着色节点数为2。

计算节点3的最大着色节点数：节点3有两个子节点，分别为节点6和节点7。由于节点6和节点7都未被染色，所以节点3的最大着色节点数为2。

计算节点4和节点5的最大着色节点数：由于节点4和节点5都未被染色，所以它们各自的最大着色节点数为0。

计算节点6和节点7的最大着色节点数：由于节点6和节点7都未被染色，所以它们各自的最大着色节点数为0。

根据动态规划的结果，二号玩家在游戏结束时的最大着色节点数为2，而一号玩家在游戏结束时的最大着色节点数为0。因此，二号玩家可以确保赢得游戏。

二叉树着色游戏是一种富有挑战性的游戏，它不仅考验玩家的逻辑思维和策略能力，还涉及到动态规划等算法知识。通过分析游戏规则和算法，我们可以找到二号玩家赢得游戏的方法。在实际应用中，二叉树着色游戏可以帮助我们更好地理解和掌握二叉树的相关知识，提高我们的编程能力。