rossler系统,非线性混沌现象解析

你知道吗？在数学的奇妙世界里，有一个名叫Rossler系统的家伙，它可是个充满魅力的存在。今天，就让我带你一起探索这个神秘的世界，揭开Rossler系统的神秘面纱。

一、初识Rossler系统：一个简单的方程组

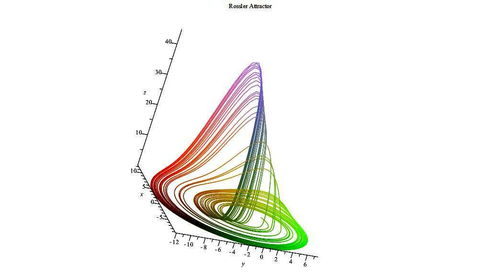
想象你手中拿着一个魔方，每个面都充满了复杂的图案。Rossler系统，这个数学界的魔方，由三个变量x、y、z和四个参数α、β、γ、ω组成。它的方程组看起来可能有些复杂，但别担心，我来给你解释一下：

\\[ \\frac{dx}{dt} = -\\omega y - z \\]

\\[ \\frac{dy}{dt} = \\omega x + \\alpha y \\]

\\[ \\frac{dz}{dt} = \\beta z + x y \\]

这些方程组就像是一张张拼图，将x、y、z三个变量紧密地联系在一起。而α、β、γ、ω这四个参数，就像是魔方的旋转轴，它们的变化会直接影响系统的行为。

二、探索混沌世界：Rossler系统的魅力

说到混沌，你可能会想到蝴蝶效应，或者那些复杂的非线性系统。而Rossler系统，正是这样一个充满混沌魅力的存在。它就像是一个顽皮的孩子，在数学的海洋中尽情地玩耍。

当参数α、β、γ、ω取特定的值时，Rossler系统会呈现出混沌现象。这意味着，即使初始条件只相差一点点，系统的行为也会随着时间的推移而变得截然不同。这种现象，被称为“蝴蝶效应”。

三、MATLAB带你走进Rossler系统

MATLAB，这个强大的数学工具，可以帮助我们更好地理解Rossler系统。通过MATLAB，我们可以绘制出系统的相图、分岔图、庞加莱截面等，从而直观地观察系统的行为。

在MATLAB中，我们可以使用龙格-库塔四阶算法来求解Rossler系统的微分方程。通过调整参数α、β、γ、ω，我们可以观察到系统从有序到混沌的转变过程。

四、Rossler系统的应用：从理论到实践

虽然Rossler系统是一个理论模型，但它却在许多领域有着广泛的应用。例如，在气象学中，它可以用来模拟大气对流；在生物学中，它可以用来研究神经元的活动；在工程学中，它可以用来分析电路的稳定性。

此外，Rossler系统还可以用来研究混沌同步现象。混沌同步是指两个或多个混沌系统在特定条件下，其行为变得一致。这一现象在通信、控制等领域有着重要的应用价值。

五、：探索数学的奇妙世界

通过探索Rossler系统，我们不仅了解了混沌现象的奥秘，还感受到了数学的无限魅力。在这个充满未知的世界里，还有无数像Rossler系统这样的奇妙存在等待我们去发现。

让我们一起，拿起数学的魔方，开启这段奇妙的旅程吧！