matlab二阶系统的阶跃响应,MATLAB环境下二阶系统阶跃响应分析与动态性能评估

你有没有想过，当你按下启动按钮的那一刻，那些复杂的机器是如何迅速而准确地响应你的指令的呢？这就是我们今天要探讨的话题——MATLAB二阶系统的阶跃响应。想象你就像是一位指挥家，而MATLAB则是你的交响乐团，通过调整参数，你可以听到不同的“乐章”。

探索MATLAB的魔法世界：什么是阶跃响应？

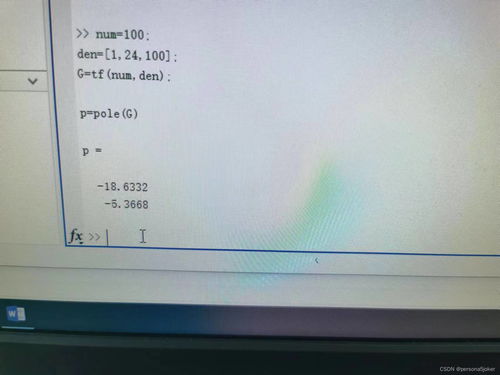
首先，让我们来揭开阶跃响应的神秘面纱。阶跃响应是控制系统分析中的一个重要概念，它描述了系统在单位阶跃输入下的输出响应。简单来说，就是当系统突然接收到一个阶跃信号时，它会如何表现。

在MATLAB中，你可以通过`step`函数来模拟这个过程。想象你给MATLAB发送了一个指令：“请绘制一个二阶系统的阶跃响应。”MATLAB就会像一位忠实的助手，计算出系统的响应，并将其绘制成曲线。

二阶系统：控制世界的灵魂

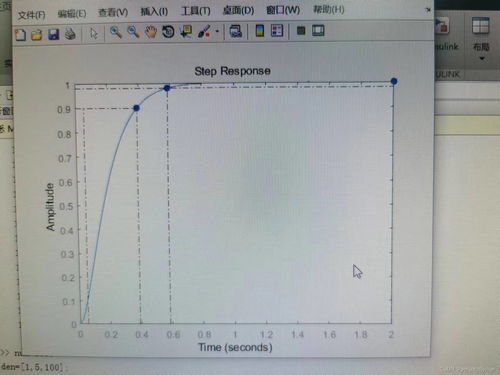
二阶系统在控制系统中扮演着至关重要的角色。它们广泛应用于各种领域，从汽车悬挂系统到机器人控制，再到复杂的工业过程控制。二阶系统的特点在于它们具有两个自由度，这使得它们能够模拟许多现实世界中的动态系统。

在MATLAB中，二阶系统的阶跃响应可以通过以下传递函数来描述：

\\[ G(s) = \\frac{K}{(s^2 + 2\\zeta\\omega_n s + \\omega_n^2)} \\]

其中，\\( K \\) 是增益，\\( \\zeta \\) 是阻尼比，\\( \\omega_n \\) 是自然频率。

MATLAB大显身手：绘制阶跃响应曲线

现在，让我们用MATLAB来绘制一个二阶系统的阶跃响应曲线。首先，你需要定义系统的参数，比如增益、阻尼比和自然频率。以下是一个简单的例子：

```matlab

num = [1]; % 分子

den = [2 1 1]; % 分母

sys = tf(num, den); % 创建传递函数

step(sys); % 绘制阶跃响应曲线

运行这段代码后，你会在MATLAB的图形窗口中看到一个曲线，它展示了系统在单位阶跃输入下的响应。你可以通过调整`num`和`den`数组中的值来改变系统的参数，从而观察不同参数对阶跃响应的影响。

深入分析：解读阶跃响应曲线

阶跃响应曲线可以提供很多关于系统性能的信息。以下是一些关键指标：

- 上升时间：系统响应从10%上升到90%所需的时间。

- 峰值时间：系统响应达到峰值所需的时间。

- 超调量：系统响应超过最终稳态值的百分比。

- 调整时间：系统响应达到并保持在最终稳态值的5%以内所需的时间。

通过分析这些指标，你可以评估系统的动态性能，并确定是否需要调整参数以改善性能。

MATLAB的强大功能：计算时域性能指标

MATLAB不仅可以帮助你绘制阶跃响应曲线，还可以自动计算时域性能指标。以下是一个计算超调量的例子：

```matlab

[y, t] = step(sys);

[C, d] = tfdata(sys, 'time');

Mp = (y(end) - C) / C 100;

disp(['超调量为：', num2str(Mp)]);

这段代码首先计算了系统的阶跃响应，然后使用`tfdata`函数提取了系统的时域数据。它计算了超调量并显示在命令窗口中。

：MATLAB与二阶系统阶跃响应的完美结合

通过MATLAB，我们可以轻松地模拟和分析二阶系统的阶跃响应。这不仅可以帮助我们理解系统的动态行为，还可以帮助我们设计出更高效、更可靠的控制系统。所以，下次当你按下启动按钮时，不妨想想MATLAB是如何帮助你实现这一奇迹的。毕竟，在这个数字化的时代，MATLAB就是你的得力助手！