matlab求系统极点,Matlab系统极点求解方法概述

你有没有想过，MATLAB这个强大的工具箱，竟然能帮你轻松找到系统的极点？没错，就是那些决定系统动态特性的神秘点！今天，就让我带你一起探索MATLAB求系统极点的奇妙之旅吧！

极点探秘：什么是极点？

在数学的世界里，极点就像是系统的灵魂，它们决定了系统在复平面上的分布，进而影响系统的稳定性、响应速度等特性。简单来说，极点就是系统传递函数分母的根，也就是那些让分母为零的“神秘数字”。

MATLAB大法：如何求极点？

MATLAB可是求极点的神器，它提供了多种方法来帮助我们找到这些神秘的极点。下面，我就来给你介绍几种常用的MATLAB求极点技巧。

1. 使用`poles`函数

`poles`函数是MATLAB中用来计算系统极点的神器。它的语法非常简单，只需要传入一个系统模型（可以是状态空间模型、传递函数模型或零极点模型）即可。

```matlab

% 定义一个传递函数模型

sys = tf([1 2],[1 3 2]);

% 计算系统的极点

p = poles(sys);

% 显示极点

disp(p);

运行这段代码，你就能看到系统的极点啦！是不是很简单？

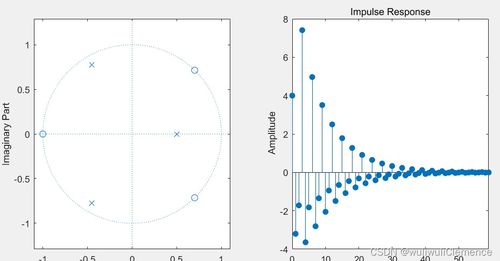
2. 使用`zplane`函数

`zplane`函数不仅可以绘制系统的零极点图，还能直接计算出极点。它的语法也很简单，只需要传入一个系统模型即可。

```matlab

% 定义一个传递函数模型

sys = tf([1 2],[1 3 2]);

% 绘制系统的零极点图

zplane(sys);

% 显示极点

disp(poles(sys));

运行这段代码，你不仅能看到系统的零极点图，还能直接获取到极点的数值。

3. 使用`freqs`函数

`freqs`函数可以计算系统的频率响应，同时也能帮助我们找到极点。它的语法如下：

```matlab

% 定义一个传递函数模型

sys = tf([1 2],[1 3 2]);

% 计算系统的频率响应

[h, w] = freqs(sys, w);

% 显示极点

disp(poles(sys));

运行这段代码，你同样可以找到系统的极点。

极点应用：极点与系统稳定性

极点不仅仅是数学上的概念，它们还与系统的稳定性息息相关。一般来说，如果系统的所有极点都位于复平面的左半部分，那么系统就是稳定的；如果存在至少一个极点位于右半部分，那么系统就是不稳定的。

MATLAB提供了`isstable`函数来帮助我们判断系统的稳定性。它的语法如下：

```matlab

% 定义一个传递函数模型

sys = tf([1 2],[1 3 2]);

% 判断系统的稳定性

if isstable(sys)

disp('系统是稳定的');

else

disp('系统是不稳定的');

运行这段代码，你就能知道你的系统是稳定还是不稳定了。

MATLAB求极点技巧：注意事项

在使用MATLAB求极点时，需要注意以下几点：

1. 确保系统模型正确无误；

2. 选择合适的求极点方法；

3. 注意极点的数值和位置；

4. 结合系统稳定性进行分析。

MATLAB求系统极点其实并不难，只要掌握了正确的方法，你就能轻松找到那些神秘的极点，并分析系统的稳定性。快来试试吧，相信你一定会爱上MATLAB求极点的奇妙之旅！