matlab求系统的阶跃响应,MATLAB求解系统阶跃响应方法详解

你有没有想过，当你按下启动按钮的那一刻，系统是如何从静止到活跃起来的呢？这就是我们今天要探讨的——MATLAB求系统的阶跃响应。想象就像一个安静的湖面被一颗石子击中，激起一圈又一圈的涟漪，系统的阶跃响应也是如此，它揭示了系统从初始状态到稳定状态的全过程。那么，如何用MATLAB来捕捉这一过程呢？让我们一起探索吧！

MATLAB：你的系统分析利器

MATLAB，这个强大的工具箱，几乎成了工程和科学领域的标配。它不仅可以帮助我们进行复杂的数学运算，还能让我们直观地看到系统的动态行为。而阶跃响应，就是其中的一项重要功能。

什么是阶跃响应？

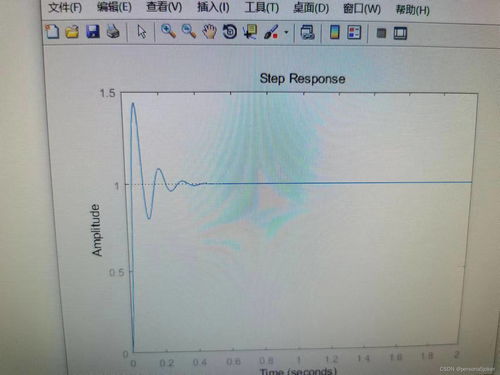
简单来说，阶跃响应就是当系统输入一个阶跃信号时，系统输出随时间的变化情况。这个阶跃信号可以理解为“突然”给系统一个变化，比如从0到1的突变。通过观察阶跃响应，我们可以了解系统的稳定性、响应速度、超调量等重要特性。

MATLAB求阶跃响应的步骤

那么，如何用MATLAB来求系统的阶跃响应呢？其实，步骤非常简单，就像做一道简单的数学题：

1. 定义系统模型：首先，你需要定义系统的数学模型。在MATLAB中，这通常是通过传递函数（Transfer Function）来实现的。传递函数描述了系统输入和输出之间的关系。

2. 使用`step`函数：一旦你有了系统的传递函数，就可以使用`step`函数来计算阶跃响应。这个函数会自动计算系统在阶跃输入下的输出。

3. 可视化结果：使用`plot`函数将结果可视化。这样，你就可以看到系统输出随时间的变化曲线了。

示例：MATLAB代码解析

让我们通过一个简单的例子来具体看看这个过程。假设我们有一个传递函数G(s) = 1 / (s + 1)，我们想要计算它的阶跃响应。

```matlab

% 定义传递函数

sys = tf([1], [1 1]);

% 计算阶跃响应

[t, y] = step(sys);

% 绘制阶跃响应曲线

plot(t, y);

title('系统的阶跃响应');

xlabel('时间 (s)');

ylabel('输出');

这段代码首先定义了一个传递函数sys，然后使用`step`函数计算了它的阶跃响应，并将结果存储在`t`和`y`中。使用`plot`函数将时间`t`和输出`y`绘制成曲线。

深入解析：阶跃响应的特性

现在，我们已经知道了如何计算阶跃响应，那么，如何解读这些结果呢？

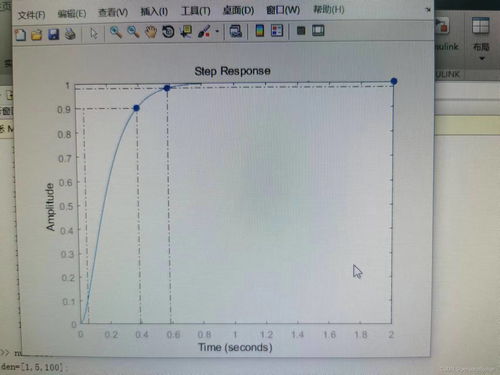
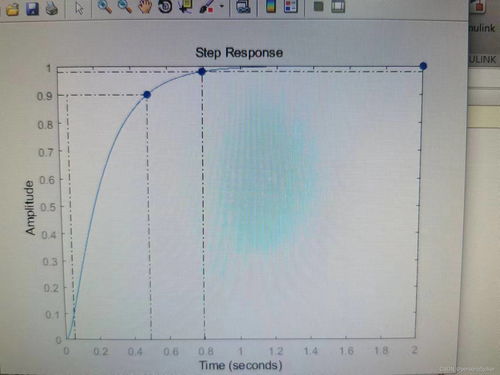
1. 上升时间：这是从阶跃响应开始到输出达到稳态值的90%所需的时间。

2. 峰值时间：这是从阶跃响应开始到输出达到峰值所需的时间。

3. 超调量：这是输出峰值与稳态值之间的差值与稳态值的比值。

4. 调整时间：这是从阶跃响应开始到输出达到并保持在稳态值的±2%范围内所需的时间。

这些特性可以帮助我们评估系统的性能，并确定它是否满足我们的设计要求。

：MATLAB求阶跃响应的实用技巧

通过以上内容，相信你已经对MATLAB求阶跃响应有了基本的了解。以下是一些实用的技巧，可以帮助你更好地使用这个功能：

- 选择合适的采样时间：采样时间太短会导致计算量大，而太长则可能无法捕捉到系统的快速变化。

- 调整时间范围：根据你的需求，调整时间范围可以让你更清晰地观察系统的动态行为。

- 使用不同的系统模型：除了传递函数，MATLAB还支持其他系统模型，如状态空间模型。根据你的需求选择合适的模型。

- 结合其他工具：MATLAB与其他工具箱，如控制系统工具箱，可以提供更丰富的功能，如稳定性分析、频率响应分析等。

MATLAB求阶跃响应是一个强大的工具，可以帮助你深入了解系统的动态行为。通过掌握这个技能，你将能够更好地设计、分析和优化系统。