matlab求系统响应曲线,MATLAB系统响应曲线求解与绘制方法概述

你有没有想过，如何让你的电脑像魔法师一样，能够预测未来的变化呢？其实，这并不是什么魔法，而是数学和计算机科学的魅力所在。今天，就让我带你走进MATLAB的世界，一起探索如何用MATLAB求系统响应曲线，让你的电脑也能“预见”未来！

MATLAB：你的系统响应曲线小助手

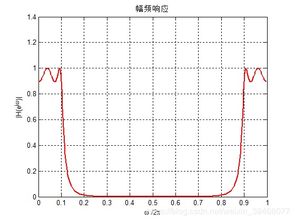
MATLAB，这个在工程和科学领域大名鼎鼎的软件，它不仅能帮你处理复杂的数学问题，还能帮你绘制出系统的响应曲线，让你直观地看到系统的动态变化。那么，如何用MATLAB求系统响应曲线呢？下面，我们就来一步步揭开这个神秘的面纱。

一、准备你的系统模型

在MATLAB中，首先你需要有一个系统的模型。这个模型可以是微分方程、传递函数，甚至是差分方程。比如，一个简单的二阶系统可以用以下微分方程来描述：

\\[ \\frac{d^2y}{dt^2} + 2\\zeta\\omega_n\\frac{dy}{dt} + \\omega_n^2y = u \\]

其中，\\( y \\) 是系统的输出，\\( u \\) 是输入，\\( \\zeta \\) 是阻尼比，\\( \\omega_n \\) 是无阻尼自然频率。

二、选择合适的求解方法

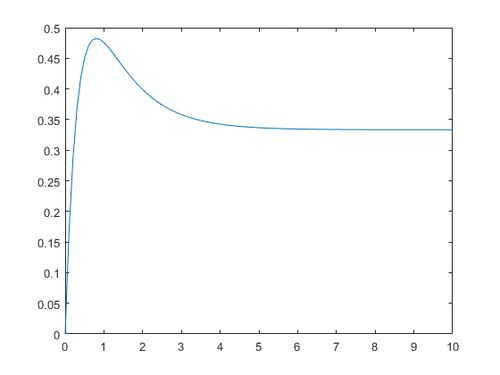
MATLAB提供了多种求解微分方程的方法，比如ode45、ode23等。ode45是最常用的一个，因为它既快又准确。下面是一个使用ode45求解上述微分方程的例子：

```matlab

t = 0:0.01:10; % 定义时间向量

y0 = [0, 1]; % 初始状态

[t, y] = ode45(@(t,y) [y(2); -2y(2) - 3y(1)], t, y0);

这段代码定义了时间向量`t`，初始状态`y0`，然后调用`ode45`函数求解微分方程，并将结果存储在`t`和`y`中。

三、绘制系统响应曲线

得到了系统的响应数据后，接下来就是绘制系统响应曲线了。MATLAB提供了丰富的绘图函数，比如`plot`、`step`等。以下是一个绘制系统响应曲线的例子：

```matlab

plot(t, y(:,1));

title('系统输出响应曲线');

xlabel('时间 t');

ylabel('输出 y');

grid on;

这段代码将绘制出系统输出`y`随时间`t`变化的曲线，并添加了标题、轴和网格。

四、分析系统性能

绘制出系统响应曲线后，你还可以进一步分析系统的性能。比如，你可以计算系统的上升时间、调节时间、超调量等。以下是一个计算系统超调量的例子：

```matlab

[y_max, max_idx] = max(y(:,1));

overshoot = (y_max - 1) 100;

disp(['系统超调量: ', num2str(overshoot), '%']);

这段代码计算了系统输出的最大值，并据此计算了系统的超调量。

五、探索更多可能性

MATLAB不仅仅能帮你求解微分方程和绘制响应曲线，它还能帮你进行更复杂的系统分析。比如，你可以使用控制系统工具箱来分析系统的稳定性、时域性能和频域性能等。

使用MATLAB求系统响应曲线其实并不复杂。你只需要准备好系统模型，选择合适的求解方法，然后绘制出响应曲线，最后分析系统的性能即可。相信通过这篇文章的介绍，你已经对MATLAB求系统响应曲线有了更深入的了解。现在，就让我们一起用MATLAB探索更多可能性吧！