matlab 混沌系统,Matlab环境下混沌系统原理与应用解析

探秘MATLAB中的混沌世界：跟随数字足迹，揭开无序中的有序

在数字的海洋中，MATLAB犹如一位智慧舵手，引领我们驶向知识的彼岸。今天，就让我们放下繁忙的工作，跟随MATLAB的脚步，一起探索那充满神秘色彩的混沌世界吧！

什么是混沌系统？

混沌，听起来是不是让人联想到无序、混乱？其实，混沌系统并非我们想象中的那样。它是一种在确定性系统中出现的复杂动态行为，具有以下特点：

1. 确定性：混沌系统遵循确定的数学规律，其行为完全由初始条件和参数决定。

2. 敏感依赖初始条件：混沌系统对初始条件极为敏感，即使初始条件有微小的差异，也会导致长期行为的巨大差异。

3. 长期行为不可预测：尽管混沌系统遵循确定的规律，但由于其敏感依赖初始条件，长期行为往往呈现出不可预测的特性。

MATLAB：混沌世界的探索者

MATLAB，作为一款功能强大的数学计算软件，在混沌系统的研究中扮演着重要角色。它不仅可以帮助我们建立混沌模型，还能通过可视化手段，让我们直观地感受混沌现象。

搭建混沌模型

在MATLAB中，我们可以通过编写代码来搭建混沌模型。以下是一个经典的Lorenz系统模型：

```matlab

function dxLorenz(t,x)

dx = [-10(x(1)-x(2)); 30x(1)-x(2)-x(1)x(3); x(1)x(2)-2.6667x(3)];

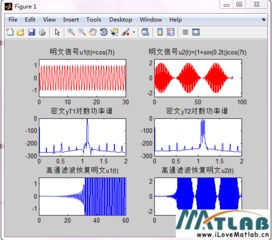
可视化混沌现象

MATLAB强大的绘图功能，让我们可以轻松地绘制出混沌系统的相图、分岔图等。以下是一个绘制Lorenz系统相图的示例：

```matlab

tspan = [0 100];

[t,x] = ode45(@dxLorenz, tspan, [0.1 0.1 0.1]);

plot3(x(:,1), x(:,2), x(:,3));

xlabel('X');

ylabel('Y');

zlabel('Z');

title('Lorenz系统相图');

庞加莱截面图：揭示混沌的奥秘

庞加莱截面图是研究混沌系统的重要工具之一。它通过对系统状态进行采样，并在相空间上绘制出来，从而揭示混沌现象的奥秘。

分岔图：参数变化下的混沌现象

分岔图是研究混沌系统参数变化对系统行为影响的重要手段。通过绘制分岔图，我们可以直观地观察到混沌现象的产生、发展和消失。

MATLAB在混沌系统研究中的应用

MATLAB在混沌系统研究中的应用非常广泛，以下是一些典型的应用场景：

1. 混沌系统的数值模拟：利用MATLAB求解微分方程，模拟混沌系统的行为。

2. 混沌系统的可视化：通过MATLAB绘制相图、分岔图等，直观地展示混沌现象。

3. 混沌系统的控制：利用MATLAB设计混沌系统的控制器，实现对混沌行为的控制。

4. 混沌系统的应用：将混沌系统应用于密码学、图像加密等领域。

MATLAB，这位数字世界的探索者，带领我们走进了混沌的奇妙世界。在这里，我们看到了无序中的有序，感受到了数学的神奇魅力。让我们继续跟随MATLAB的脚步，探索更多未知的领域吧！