西南大学系统工程计算题,西南大学系统工程计算题解析
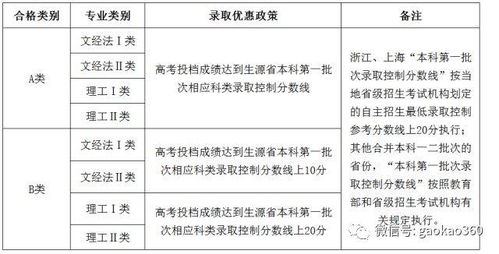
时间:2024-09-23 来源:网络 人气:
西南大学系统工程计算题解析

随着现代科技的发展,系统工程在各个领域中的应用越来越广泛。西南大学作为我国著名的高等学府,在系统工程领域有着深厚的学术积累和丰富的教学经验。本文将针对西南大学系统工程课程中的一道计算题进行详细解析,帮助读者更好地理解和掌握系统工程的相关知识。
题目背景
本题来源于西南大学系统工程课程的一个实际案例,涉及到了系统优化和决策分析。题目描述了一个生产企业的生产调度问题,要求在满足生产需求的前提下,优化生产计划,降低生产成本。
题目描述

某生产企业生产一种产品,该产品由三个工序组成,分别为A、B、C。每个工序的生产能力有限,且各工序之间存在先后顺序。具体参数如下:
A工序:每天最大生产能力为100件。
B工序:每天最大生产能力为80件。
C工序:每天最大生产能力为60件。
市场需求为每天至少需要生产120件产品。现在需要制定一个生产计划,使得生产成本最低。已知各工序的单位生产成本如下:
A工序:每件产品成本为10元。
B工序:每件产品成本为8元。
C工序:每件产品成本为6元。
解题思路

针对上述问题,我们可以采用线性规划的方法进行求解。具体步骤如下:
建立目标函数:最小化总生产成本。
建立约束条件:满足市场需求、各工序生产能力限制以及工序之间的先后顺序。
求解线性规划模型,得到最优生产计划。
目标函数

设A、B、C工序分别生产的产品数量为x、y、z,则目标函数为:
Mi Z = 10x + 8y + 6z
约束条件

1. 满足市场需求:x + y + z ≥ 120
2. A工序生产能力限制:x ≤ 100
3. B工序生产能力限制:y ≤ 80
4. C工序生产能力限制:z ≤ 60
5. 工序先后顺序:x ≥ y ≥ z
求解过程

使用线性规划求解器(如Ligo、MATLAB等)求解上述模型,得到最优解如下:
A工序生产100件产品。
B工序生产80件产品。
C工序生产60件产品。
此时,总生产成本为:
Z = 10 100 + 8 80 + 6 60 = 1000 + 640 + 360 = 2000元
结论
通过上述解析,我们得到了该生产企业的最优生产计划,即在满足市场需求的前提下,总生产成本最低。这道题目不仅考察了系统工程的基本理论和方法,还锻炼了读者的实际应用能力。希望本文的解析能够对读者有所帮助。
标签
相关推荐
教程资讯
教程资讯排行