rossler系统,非线性混沌现象解析

嗨，亲爱的读者们，今天我要带你们踏上一段奇妙的数学之旅，探索一个充满神秘色彩的数学世界——Rossler系统。这个系统虽然听起来有些高深莫测，但其实它就在我们身边，只是我们平时没有注意到它罢了。让我们一起揭开它的神秘面纱，看看这个系统到底有什么特别之处吧！

混沌的起源：从Lorenz到Rossler

要了解Rossler系统，我们不得不先提到它的前辈——Lorenz系统。Lorenz系统是一个描述大气对流的简化模型，由三个微分方程构成。这个系统在1963年被Lorenz发现，它揭示了混沌现象的奥秘。而Rossler系统，则是由德国物理学家Eugenio Rossler在1976年提出的，它比Lorenz系统更加简单，但同样能够展现出混沌的美丽。

Rossler系统的方程

Rossler系统的方程如下：

\\[ \\frac{dx}{dt} = -y - z \\]

\\[ \\frac{dy}{dt} = x + ay \\]

\\[ \\frac{dz}{dt} = b + z(x - c) \\]

其中，\\( x \\)、\\( y \\)、\\( z \\) 是系统的三个变量，\\( a \\)、\\( b \\)、\\( c \\) 是系统参数。这些参数的取值不同，系统表现出的行为也会有所不同。

混沌吸引子：一个旋转的“心”

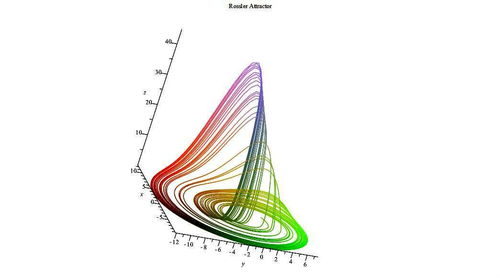
当系统参数取特定值时，Rossler系统会进入一个稳定的混沌状态。在这个状态下，系统的轨迹会在一个称为“混沌吸引子”的复杂结构中不断旋转。这个吸引子看起来像是一个旋转的“心”，因此也被称为“旋转吸引子”。

单心结构：简化混沌同步

与Lorenz系统相比，Rossler系统的吸引子具有一个显著的特点——单心结构。这意味着吸引子只有一个中心点，这使得混沌同步的研究变得更加简单。混沌同步是指将两个或多个混沌系统连接起来，使它们的轨迹保持一致。在Rossler系统中，单心结构大大简化了混沌同步问题的研究。

参数的影响：从有序到混沌

在Rossler系统中，参数的取值对系统的行为有着重要的影响。当参数取特定值时，系统会表现出有序的运动，如周期运动或准周期运动。当参数发生微小变化时，系统可能会突然进入混沌状态。这种现象被称为“分岔”，是混沌理论中的一个重要概念。

可视化：探索混沌之美

为了更好地理解Rossler系统的行为，我们可以通过可视化来观察它的轨迹。在MATLAB等软件中，我们可以绘制出系统的相图、分岔图和庞加莱截面等图形，从而直观地看到系统的运动轨迹和混沌吸引子的形状。

应用：从物理到生物

Rossler系统不仅在数学和物理学领域有着广泛的应用，还在生物学、化学等领域有着重要的应用。例如，它可以用来模拟心脏的跳动、化学反应的动力学等。

：探索未知的魅力

通过探索Rossler系统，我们不仅能够领略到混沌现象的美丽，还能够了解到数学在各个领域的广泛应用。这个充满神秘色彩的数学世界，等待着我们去发现、去探索。让我们一起踏上这段奇妙的旅程，揭开更多未知的奥秘吧！