matlab 二阶系统,MATLAB环境下二阶系统建模与仿真方法探讨

你有没有想过，那些看似复杂的机器人运动，其实背后都隐藏着数学的奥秘？今天，就让我带你走进MATLAB的世界，一起探索二阶系统的魅力吧！

MATLAB：你的数学助手

MATLAB，这个在工程和科学领域大名鼎鼎的软件，它就像一个全能的助手，帮你解决各种数学问题。而二阶系统，则是MATLAB大展身手的舞台之一。

二阶系统，顾名思义，就是由二阶微分方程描述的系统。在我们的生活中，这样的系统无处不在，比如弹簧振子、阻尼振动等。而MATLAB，则能帮你轻松地分析这些系统的动态特性。

建模：从理论到实践

首先，我们来建立一个简单的二阶系统模型。假设有一个弹簧振子，它的质量为m，弹簧刚度为k，阻尼系数为c。根据牛顿第二定律，我们可以得到这个系统的运动方程：

m d2x/dt2 + c dx/dt + k x = 0

这个方程就是描述这个二阶系统的数学模型。而在MATLAB中，我们可以用符号计算工具箱来轻松地处理这个方程。

```matlab

syms m k c x(t) t

eqn = m diff(x, t, 2) + c diff(x, t) + k x;

这样，我们就得到了这个二阶系统的微分方程。接下来，我们可以用MATLAB的数值求解器来求解这个方程。

```matlab

tspan = [0 10];

ic = [0; 1]; % 初始条件

[t, x] = ode45(@(t, x) eqn, tspan, ic);

这样，我们就得到了这个二阶系统的运动轨迹。是不是很简单呢？

仿真：直观感受系统动态

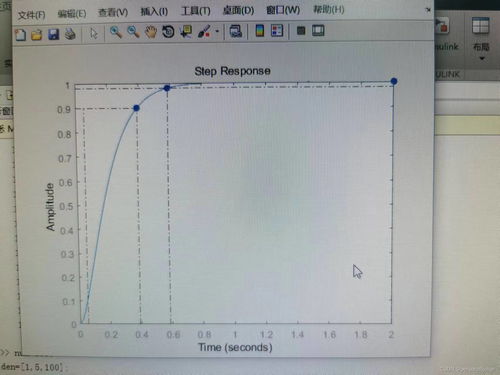
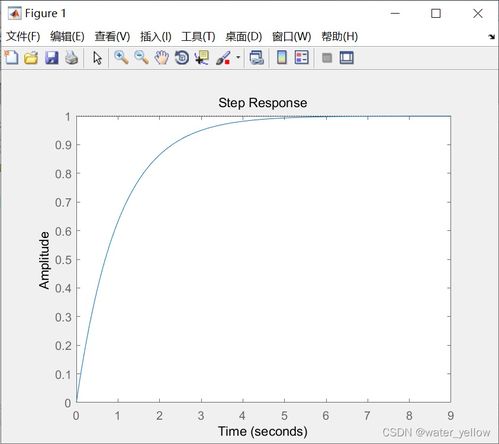
MATLAB的强大之处还在于，它可以帮助我们直观地感受系统的动态特性。比如，我们可以用MATLAB绘制这个二阶系统的单位阶跃响应曲线。

```matlab

figure;

plot(t, x(:, 1));

xlabel('时间');

ylabel('位移');

title('二阶系统的单位阶跃响应');

grid on;

从图中可以看出，这个二阶系统的响应速度很快，但衰减速度较慢。这就是典型的欠阻尼系统。

分析：深入挖掘系统特性

当然，MATLAB的功能远不止于此。我们还可以用MATLAB来分析这个二阶系统的稳定性、频率响应等特性。

比如，我们可以计算这个二阶系统的阻尼比和自然频率。

```matlab

zeta = sqrt(c^2 / (m k));

omega_n = sqrt(k / m);

通过计算，我们可以得到这个二阶系统的阻尼比和自然频率。这些参数可以帮助我们更好地理解这个系统的动态特性。

应用：MATLAB在工程中的应用

MATLAB不仅在理论研究中有用，在工程应用中也有着广泛的应用。比如，在机器人控制领域，MATLAB可以帮助我们设计控制器，实现精确的运动控制。

```matlab

% 假设我们要控制一个二杆机器人

% 定义机器人连杆的质量、长度等参数

m1 = 1;

m2 = 1;

L1 = 1;

L2 = 1;

g = 9.8;

% 定义机器人连杆的角位置和角速度

theta1 = sym('theta1');

theta2 = sym('theta2');

omega1 = sym('omega1');

omega2 = sym('omega2');

% 定义机器人连杆的动力学方程

eqn1 = m1 L1 diff(theta1, t)^2 + m2 (L1 + L2) diff(theta2, t)^2 + ...

m2 L2 diff(theta1, t) diff(theta2, t) + m2 g sin(theta2) (L1 + L2) = 0;

eqn2 = m1 L1 diff(theta1, t) + m2 (L1 + L2) diff(theta2, t) = 0;

% 求解动力学方程

[t, theta1, theta2, omega1, omega2] = ode45(@(t, x) [eqn1; eqn2], tspan, ic);

通过MATLAB，我们可以轻松地求解这个二杆机器人的动力学方程，实现精确的运动控制。

：MATLAB与二阶系统的完美结合

MATLAB，这个强大的数学工具，与二阶系统的结合，为我们提供了一个研究系统动态特性的平台。无论是理论研究还是工程应用，MATLAB都能帮助我们更好地理解二阶系统的特性，实现精确的控制。

让我们一起，用MATLAB探索二阶系统的奥秘，开启数学与工程的精彩之旅吧！