matlab 系统冲激响应,MATLAB系统冲激响应求解方法与实例分析

你有没有想过，当你按下MATLAB的运行按钮，那些神秘的数学公式是如何变成生动的波形图的呢？今天，就让我带你一探究竟，揭开MATLAB系统冲激响应的神秘面纱！

冲激响应：系统的心跳

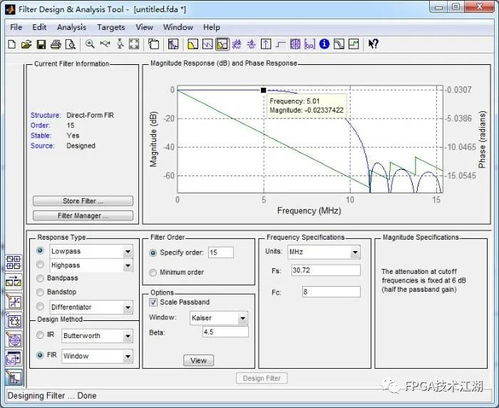
想象一个系统就像一个心脏，而冲激响应就是它跳动的节奏。在MATLAB的世界里，冲激响应是衡量系统性能的重要指标。它描述了系统对单位冲激信号的响应，就像医生通过听诊器听心脏的跳动一样。

MATLAB：冲激响应的魔术师

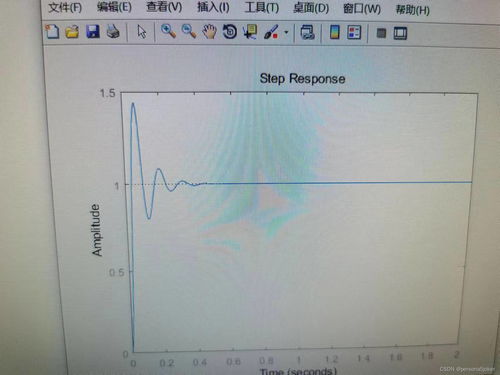
MATLAB，这个强大的工具箱，拥有一个神奇的函数——impulse。它就像一个魔术师，只需几行代码，就能让系统的冲激响应跃然屏幕之上。

impulse函数的奥秘

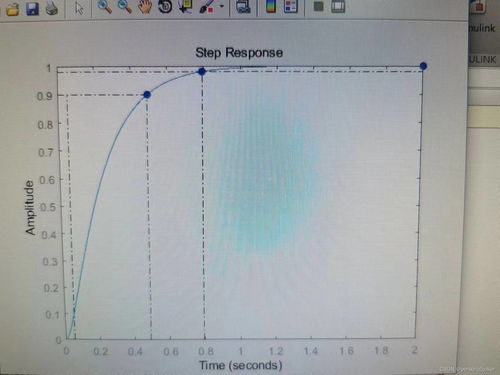
impulse函数的用法简单到令人难以置信。你只需要提供系统的分子系数（b）和分母系数（a），再指定一个时间向量（t），它就能计算出冲激响应，并绘制出相应的波形图。

举个例子

假设我们有一个RLC串联振荡电路，其系统函数如下：

\\[ H(s) = \\frac{1}{s^2 + 2\\omega_0 s + \\omega_0^2} \\]

其中，\\( \\omega_0 \\) 是自然角频率。我们可以用MATLAB来计算它的冲激响应：

```matlab

L = 22e-3; % 电感，单位：亨利

C = 2e-9; % 电容，单位：法拉

R = 100; % 电阻，单位：欧姆

omega0 = 1/sqrt(LC); % 自然角频率

% 系统分子系数

b = [1];

% 系统分母系数

a = [omega0^2, 2omega0, 1];

% 时间向量

t = 0:1e-6:8e-4;

% 计算冲激响应

h = impulse(b, a, t);

% 绘制冲激响应波形

plot(t, h);

xlabel('时间 (s)');

ylabel('冲激响应');

title('RLC串联振荡电路的冲激响应');

运行这段代码，你就能看到RLC串联振荡电路的冲激响应波形了。

冲激响应的启示

通过观察冲激响应波形，我们可以了解系统的许多特性：

1. 稳定性：如果冲激响应在有限时间内收敛，那么系统是稳定的；如果发散，那么系统是不稳定的。

2. 频率响应：冲激响应的频率成分可以告诉我们系统的频率特性。

3. 瞬态响应：冲激响应的初始部分可以反映系统的瞬态响应。

MATLAB：冲激响应的利器

MATLAB不仅可以帮助我们计算冲激响应，还可以进行更深入的分析：

1. 快速傅里叶变换（FFT）：将冲激响应进行FFT变换，可以得到系统的频谱。

2. 拉普拉斯变换：将冲激响应进行拉普拉斯变换，可以得到系统的传递函数。

3. 零点和极点：通过分析冲激响应，可以找到系统的零点和极点，从而了解系统的结构。

冲激响应：MATLAB的宝藏

MATLAB的impulse函数就像一个宝藏，它让我们可以轻松地探索系统的冲激响应。通过这个宝藏，我们可以更好地理解系统的特性，为我们的工程实践提供有力的支持。

说了这么多，你是不是已经对MATLAB的冲激响应有了更深的了解呢？快来试试吧，相信你一定会爱上这个神奇的函数！