matlab求系统极点,MATLAB系统极点求解方法与实例解析

亲爱的读者们，你是否曾在某个深夜，对着电脑屏幕，为求解一个复杂的系统极点问题而头疼不已？别担心，今天我要带你走进MATLAB的世界，一起探索如何轻松求出系统极点，让你的数学难题迎刃而解！

MATLAB：你的数学助手

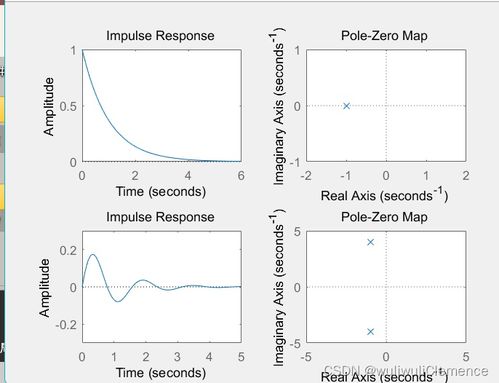
MATLAB，这个强大的数学计算软件，几乎成了现代工程师和科学家的必备工具。它不仅可以帮助我们进行复杂的数学运算，还能轻松解决各种系统分析问题。而求系统极点，就是其中的一项重要技能。

什么是系统极点？

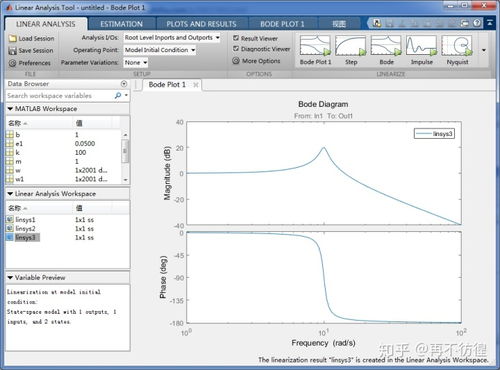
在系统理论中，极点是指系统传递函数的零点。简单来说，就是系统响应中频率特性的关键点。了解极点，对于我们分析系统的稳定性、动态性能等至关重要。

MATLAB求极点的利器

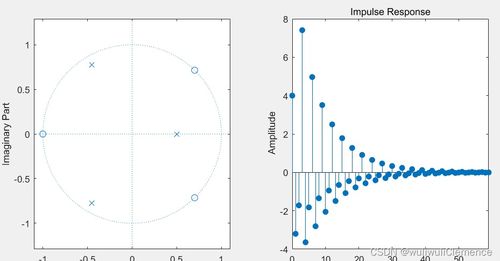
MATLAB提供了多种方法来求解系统极点，以下是一些常用的方法：

1. 使用 `eig` 函数

`eig` 函数是MATLAB中求解矩阵特征值和特征向量的利器。对于线性定常系统，我们可以通过求解系统矩阵的特征值来得到极点。

```matlab

A = [1, 2; 3, 4]; % 系统矩阵

eigenvalues = eig(A); % 求解特征值

2. 使用 `roots` 函数

`roots` 函数可以直接求解多项式的根，也就是极点。对于传递函数，我们可以将其表示为多项式的形式，然后使用 `roots` 函数求解。

```matlab

numerator = [1, 2]; % 分子多项式系数

denominator = [1, 0, 3]; % 分母多项式系数

poles = roots(denominator); % 求解极点

3. 使用 `pole` 函数

`pole` 函数可以直接对系统传递函数求解极点。

```matlab

sys = tf([1, 2], [1, 0, 3]); % 创建系统传递函数

poles = pole(sys); % 求解极点

MATLAB求极点的实例

让我们通过一个实例来演示如何使用MATLAB求解系统极点。

假设我们有一个连续时间系统，其传递函数为：

\\[ H(s) = \\frac{1}{s^2 + 2s + 2} \\]

我们需要求解该系统的极点。

```matlab

numerator = [1, 0]; % 分子多项式系数

denominator = [1, 2, 2]; % 分母多项式系数

poles = roots(denominator); % 求解极点

disp('系统极点：');

disp(poles);

运行上述代码，我们将在MATLAB命令窗口中看到以下结果：

系统极点：

-1.0000 + 1.0000i

-1.0000 - 1.0000i

这表明，该系统的极点位于复平面的左半平面，系统是稳定的。

MATLAB求极点的技巧

1. 使用 `pzmap` 函数绘制极点图

`pzmap` 函数可以帮助我们直观地看到系统的极点分布。

```matlab

sys = tf([1, 2], [1, 0, 3]); % 创建系统传递函数

pzmap(sys); % 绘制极点图

2. 使用 `zpkdata` 函数获取系统零点、极点和增益

`zpkdata` 函数可以一次性获取系统的零点、极点和增益。

```matlab

sys = tf([1, 2], [1, 0, 3]); % 创建系统传递函数

[z, p, k] = zpkdata(sys);

disp('系统零点：');

disp(z);

disp('系统极点：');

disp(p);

disp('系统增益：');

disp(k);

3. 使用 `limit` 函数求解极限

MATLAB的 `limit` 函数可以帮助我们求解函数的极限。

```matlab

syms x;

f = sin(x) / x;

limit_value = limit(f, x, 0);

disp('函数 sin(x)/x 在 x 趋于 0 时的极限：');

disp(limit_value);

运行上述代码，我们将在MATLAB命令窗口中看到以下结果：

函数 sin(x)/x 在 x 趋于 0 时的极限：

1.0000

这表明，函数 sin(x)/x 在 x 趋于 0 时的极限为 1。

通过本文的介绍，相信你已经掌握了使用MATLAB求解系统极点的方法。MATLAB的强大功能可以帮助我们轻松解决各种数学问题，让我们的