matlab 系统零输入响应,零输入响应的定义与性质

在信号与系统领域，系统响应分析是研究系统对输入信号响应特性的重要方法。其中，零输入响应是指系统在没有外部激励信号作用下的自然响应。本文将利用MATLAB软件对线性时不变（LTI）系统的零输入响应进行详细分析，并通过实例展示如何使用MATLAB进行相关计算和图形展示。

零输入响应的定义与性质

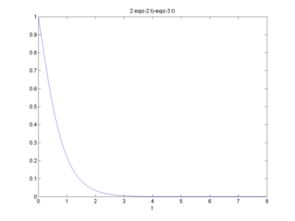
零输入响应是指系统在没有外部激励信号作用下的自然响应。对于线性时不变系统，其零输入响应可以通过求解系统的微分方程得到。根据线性时不变系统的性质，零输入响应满足以下特点：

线性：零输入响应是系统输入信号的线性组合。

时不变性：系统的零输入响应不随时间变化而改变。

因果性：系统的零输入响应仅由系统初始状态决定，与系统历史输入无关。

使用MATLAB求解零输入响应

在MATLAB中，我们可以使用以下步骤求解线性时不变系统的零输入响应：

定义系统的微分方程或传递函数。

使用`lsim`函数计算系统的零输入响应。

使用`plot`函数绘制零输入响应的图形。

实例分析

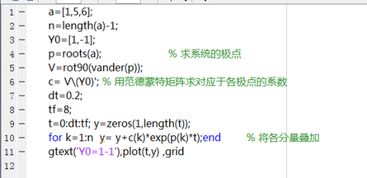
以下是一个简单的实例，展示如何使用MATLAB求解一个二阶LTI系统的零输入响应。

syms t y;

% 定义系统的微分方程

d2y_dt2 - 2d2y_dt + y = 0;

% 求解系统的零输入响应

[y, t] = lsim(d2y_dt2, [], t);

% 绘制零输入响应的图形

plot(t, y);

xlabel('时间 (s)');

ylabel('y(t)');

title('二阶LTI系统的零输入响应');

在上面的代码中，我们首先定义了一个二阶LTI系统的微分方程。使用`lsim`函数计算系统的零输入响应，并将结果存储在变量`y`和`t`中。使用`plot`函数绘制零输入响应的图形。

图形展示

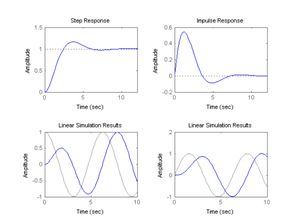
在MATLAB中，我们可以通过以下步骤将零输入响应的图形进行展示：

使用`plot`函数绘制零输入响应的图形。

使用`grid on`命令添加网格线，以便更好地观察图形。

本文介绍了使用MATLAB求解线性时不变系统零输入响应的方法。通过实例分析，展示了如何定义系统的微分方程、计算零输入响应以及绘制图形。在实际应用中，我们可以根据需要调整系统参数和输入信号，以便更好地研究系统的响应特性。