matlab 系统阶跃响应曲线,准备阶段

在自动控制系统中，阶跃响应是评估系统动态性能的重要手段。阶跃响应曲线能够直观地展示系统在受到阶跃输入时的响应过程，包括上升时间、超调量、调整时间等关键性能指标。MATLAB作为一种强大的数学计算和仿真软件，提供了丰富的工具和函数来绘制和分析系统的阶跃响应曲线。本文将详细介绍如何使用MATLAB进行系统阶跃响应曲线的绘制和分析。

准备阶段

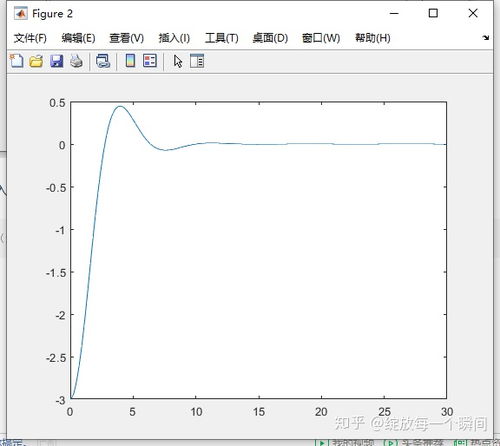
在进行阶跃响应曲线的绘制和分析之前，我们需要完成以下准备工作：

安装MATLAB软件及其控制系统工具箱（Control System Toolbox）。

确定要分析的系统的传递函数。

设置仿真参数，如仿真时间、采样时间等。

绘制阶跃响应曲线

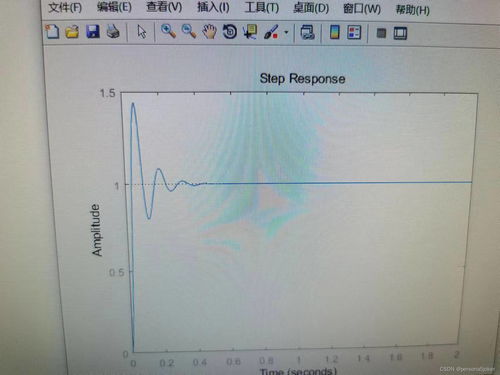
在MATLAB中，我们可以使用`step`函数来绘制系统的阶跃响应曲线。以下是一个简单的示例代码：

num = [1]; % 分子多项式系数向量

den = [1 2 2]; % 分母多项式系数向量

sys = tf(num, den); % 创建传递函数

step(sys); % 绘制阶跃响应曲线

在上面的代码中，我们首先定义了传递函数的分子和分母多项式系数，然后使用`tf`函数创建了一个传递函数对象`sys`。调用`step`函数并传入`sys`对象，即可绘制出系统的阶跃响应曲线。

分析阶跃响应曲线

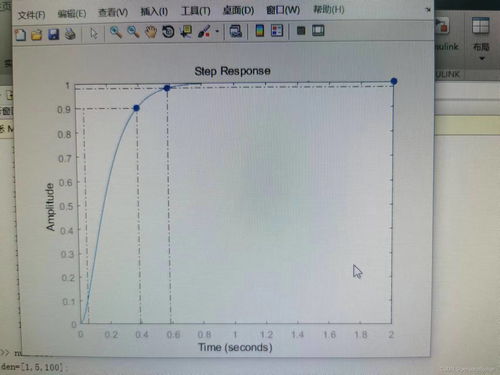
绘制出阶跃响应曲线后，我们可以通过以下方法分析系统的动态性能：

上升时间（Rise Time）：阶跃响应曲线从初始值上升到稳态值的90%所需的时间。

超调量（Overshoot）：阶跃响应曲线达到稳态值时的最大偏差与稳态值之比。

调整时间（Settling Time）：阶跃响应曲线达到并保持在稳态值±2%范围内的时间。

在MATLAB中，我们可以使用`stepinfo`函数来获取阶跃响应曲线的性能指标。以下是一个示例代码：

info = stepinfo(sys);

disp('上升时间：');

disp(info.RiseTime);

disp('超调量：');

disp(info.Overshoot);

disp('调整时间：');

disp(info.SettlingTime);

在上面的代码中，我们使用`stepinfo`函数获取了阶跃响应曲线的性能指标，并使用`disp`函数将它们打印到控制台。

修改系统参数

在实际应用中，我们可能需要修改系统的参数来优化其动态性能。在MATLAB中，我们可以通过修改传递函数的分子和分母多项式系数来实现。以下是一个示例代码，展示了如何修改系统参数并重新绘制阶跃响应曲线：

num = [1 3]; % 修改分子多项式系数

den = [1 2 2]; % 修改分母多项式系数

sys_modified = tf(num, den); % 创建修改后的传递函数

step(sys_modified); % 绘制修改后的阶跃响应曲线

在上面的代码中，我们修改了传递函数的分子多项式系数，并使用`tf`函数创建了一个新的传递函数对象`sys_modified`。调用`step`函数并传入`sys_modified`对象，即可绘制出修改后的阶跃响应曲线。

结论

本文介绍了如何使用MATLAB绘制和分析系统阶跃响应曲线。通过MATLAB的`step`函数和`stepinfo`函数，我们可以方便地获取系统的动态性能指标，并通过对系统参数的修改来优化其性能。在实际应用中，阶跃响应曲线是评估控制系统性能的重要工具，而MATLAB则为这一过程提供了强大的支持。