matlab 系统零状态响应,零状态响应的定义

在信号与系统领域，系统响应的分析是至关重要的。其中，零状态响应是系统分析中的一个基本概念，它描述了系统在无初始状态的情况下，对于给定输入信号的响应。本文将详细介绍如何在MATLAB中求解系统的零状态响应，并通过实例进行演示。

零状态响应的定义

零状态响应是指系统在无初始状态（即初始条件为零）的情况下，对于给定输入信号的响应。数学上，零状态响应可以通过求解系统的微分方程得到。对于一个线性时不变（LTI）系统，其零状态响应可以表示为：

[ y(t) = mathcal{L}^{-1}{H(s)F(s)} ]

其中，( y(t) ) 是系统的零状态响应，( H(s) ) 是系统的传递函数，( F(s) ) 是输入信号的拉普拉斯变换，( mathcal{L}^{-1} ) 表示拉普拉斯逆变换。

MATLAB中的求解方法

在MATLAB中，我们可以使用以下方法求解系统的零状态响应：

使用 `lsim` 函数：该函数可以直接求解系统的零状态响应，其调用格式为 `lsim(b, a, x, t)`，其中 `b` 和 `a` 分别是系统微分方程的系数向量，`x` 是输入信号，`t` 是时间向量。

使用 `tf` 函数：该函数可以创建系统的传递函数模型，其调用格式为 `sys = tf(b, a)`，其中 `b` 和 `a` 分别是系统传递函数的分子和分母系数。

使用 `laplace` 函数：该函数可以计算信号的拉普拉斯变换，其调用格式为 `LaplaceTransform(f, t, s)`，其中 `f` 是输入信号，`t` 是时间变量，`s` 是复频域变量。

使用 `ilaplace` 函数：该函数可以计算信号的拉普拉斯逆变换，其调用格式为 `ilaplace(Y, s, t)`，其中 `Y` 是拉普拉斯变换后的信号，`s` 是复频域变量，`t` 是时间变量。

实例演示

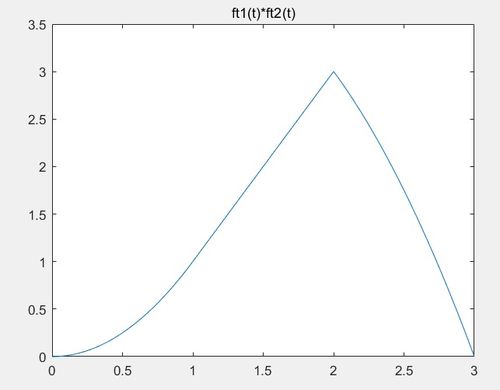
以下是一个使用MATLAB求解系统零状态响应的实例：

```matlab

% 定义系统微分方程系数

b = [1, 2, 3];

a = [1, -2, 1];

% 定义输入信号

f = @(t) sin(2pit);

% 计算输入信号的拉普拉斯变换

F = laplace(f, t, s);

% 创建系统传递函数模型

sys = tf(b, a);

% 求解系统的零状态响应

y = lsim(sys, F, 0:0.01:5);

% 绘制系统的零状态响应

plot(0:0.01:5, y);

xlabel('Time (s)');

ylabel('Zero-States Response');

title('Zero-States Response of the System');

结果分析

在上面的实例中，我们定义了一个二阶系统，其微分方程系数为 ( b = [1, 2, 3] ) 和 ( a = [1, -2, 1] )。输入信号是一个正弦信号 ( f(t) = sin(2pi t) )。通过使用 `lsim` 函数，我们计算了系统的零状态响应，并将其绘制在图中。从图中可以看出，系统的零状态响应是一个衰减的正弦波，其振幅随时间逐渐减小。

本文介绍了如何在MATLAB中求解系统的零状态响应。通过使用 `lsim` 函数和相关的拉普拉斯变换函数，我们可以方便地计算和分析系统的零状态响应。在实际应用中，掌握这些方法对于理解和设计信号与系统具有重要意义。