spss 系统聚类分析,原理、方法与应用

SPSS系统聚类分析：原理、方法与应用

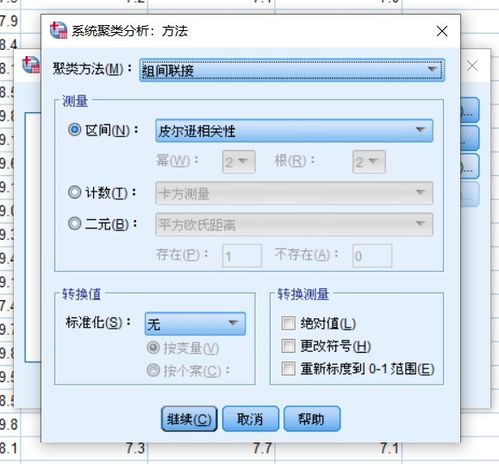
随着大数据时代的到来，数据分析在各个领域都发挥着越来越重要的作用。SPSS作为一款功能强大的统计分析软件，在数据挖掘、市场研究、社会科学等领域有着广泛的应用。本文将详细介绍SPSS系统聚类分析的基本原理、常用方法以及实际应用。

一、系统聚类分析的基本原理

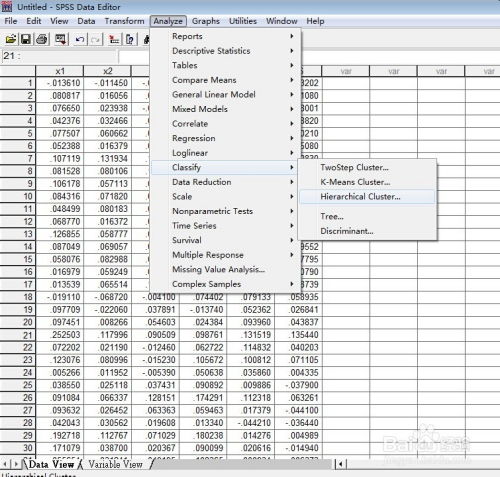
系统聚类分析是一种无监督的聚类方法，它根据样本之间的相似性或差异性，将数据集划分为若干个类别。其基本原理如下：

将所有样本视为一个类，称为初始类。

计算初始类中任意两个样本之间的距离，选择距离最近的两个样本合并为一个新类。

重复步骤2，每次合并一个新类，直到所有样本都被合并为一个类。

根据合并过程中样本之间的距离，绘制聚类树状图，直观地展示聚类过程。

二、SPSS系统聚类分析的方法

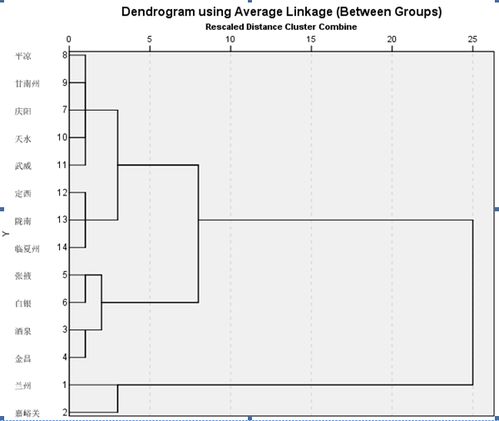
SPSS系统聚类分析提供了多种方法，以下列举几种常用方法：

欧氏距离：根据样本之间的欧氏距离进行聚类，适用于连续型变量。

曼哈顿距离：根据样本之间的曼哈顿距离进行聚类，适用于连续型变量。

切比雪夫距离：根据样本之间的切比雪夫距离进行聚类，适用于连续型变量。

最大距离：根据样本之间的最大距离进行聚类，适用于连续型变量。

最小距离：根据样本之间的最小距离进行聚类，适用于连续型变量。

三、SPSS系统聚类分析的实际应用

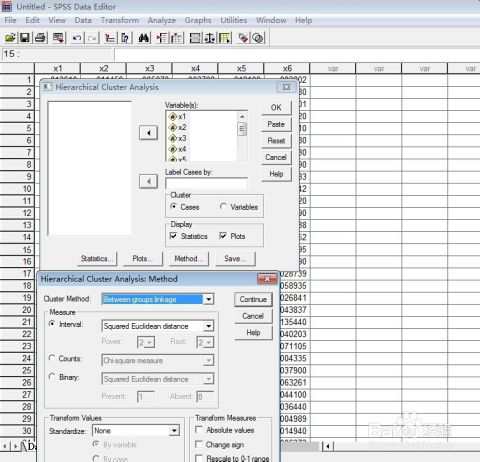
系统聚类分析在各个领域都有广泛的应用，以下列举几个实例：

市场研究：通过对消费者数据的聚类分析，可以识别出具有相似消费习惯的客户群体，为企业制定精准营销策略提供依据。

社会科学：通过对社会调查数据的聚类分析，可以识别出具有相似社会特征的群体，为政策制定提供参考。

生物信息学：通过对基因表达数据的聚类分析，可以识别出具有相似表达模式的基因，为疾病诊断和治疗提供线索。

金融分析：通过对金融数据的聚类分析，可以识别出具有相似风险特征的资产，为投资决策提供参考。

四、SPSS系统聚类分析的注意事项

在进行系统聚类分析时，需要注意以下几点：

数据预处理：对数据进行标准化处理，消除量纲的影响。

选择合适的距离度量方法：根据数据类型和特点选择合适的距离度量方法。

选择合适的聚类方法：根据数据类型和特点选择合适的聚类方法。

聚类结果解释：对聚类结果进行合理的解释，避免主观臆断。

SPSS系统聚类分析是一种无监督的聚类方法，在各个领域都有广泛的应用。本文介绍了系统聚类分析的基本原理、常用方法以及实际应用，并提醒了在使用过程中需要注意的几点。希望本文对读者有所帮助。