matlab系统离散化,理论与实践

MATLAB系统离散化：理论与实践

随着计算机技术的飞速发展，MATLAB作为一种强大的数学计算软件，在各个领域得到了广泛应用。在控制系统设计中，离散化是系统建模和分析的重要步骤。本文将详细介绍MATLAB系统离散化的方法、步骤以及在实际应用中的注意事项。

在现实世界中，许多系统都是连续的，如温度、压力、速度等。计算机只能处理离散的数值，因此需要对连续系统进行离散化处理。离散化是将连续系统转换为离散系统，以便在计算机上进行建模和分析。MATLAB提供了丰富的工具和函数，可以方便地进行系统离散化。

二、MATLAB系统离散化方法

在MATLAB中，系统离散化主要有以下几种方法：

1. 零阶保持器（Zero-Order Hold, ZOH）

零阶保持器是一种常用的离散化方法，它将连续信号在每个采样时刻的值保持一段时间。在MATLAB中，可以使用`c2d`函数实现ZOH离散化。

2. 一阶保持器（First-Order Hold, FOH）

一阶保持器在ZOH的基础上，对连续信号进行线性插值，以更精确地表示信号。在MATLAB中，可以使用`c2d`函数实现FOH离散化。

3. 双线性变换（Tustin's Method）

双线性变换是一种常用的离散化方法，它将连续信号通过双线性变换转换为离散信号。在MATLAB中，可以使用`c2d`函数实现双线性变换离散化。

4. 零极点匹配法（Zero-Pole Matching）

零极点匹配法是一种基于连续系统传递函数的离散化方法。它通过调整离散系统的零极点，使离散系统的频率响应与连续系统相似。在MATLAB中，可以使用`c2d`函数实现零极点匹配法离散化。

三、MATLAB系统离散化步骤

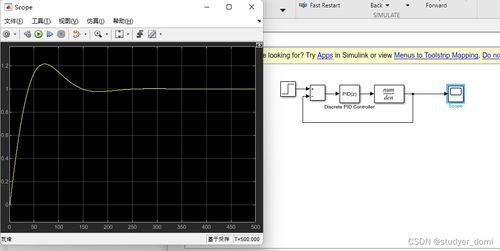
以下是使用MATLAB进行系统离散化的基本步骤：

建立连续系统的数学模型，如传递函数、状态空间模型等。

确定采样周期T。

选择合适的离散化方法。

使用`c2d`函数进行离散化。

对离散化后的系统进行仿真和分析。

四、MATLAB系统离散化实例

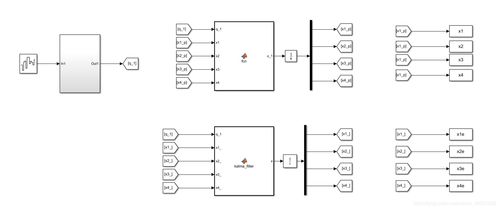
以下是一个使用MATLAB进行系统离散化的实例：

% 建立连续系统传递函数

s = tf('s');

sys = 1/(s^2 + 2s + 1);

% 确定采样周期

T = 0.1;

% 使用双线性变换进行离散化

sysd = c2d(sys, T, 'tustin');

% 仿真离散化后的系统

step(sysd);

在上面的代码中，我们首先建立了连续系统的传递函数，然后确定了采样周期T。接着，我们使用双线性变换方法对系统进行离散化，并使用`step`函数对离散化后的系统进行仿真。

五、注意事项

在使用MATLAB进行系统离散化时，需要注意以下几点：

选择合适的离散化方法，以确保离散化后的系统与连续系统相似。

确定合适的采样周期，以避免混叠现象。

对离散化后的系统进行仿真和分析，以验证其性能。

MATLAB系统离散化是控制系统设计中的重要步骤。通过本文的介绍，读者可以了解到MATLAB系统离散化的方法、步骤以及注意事项。在实际应用