matlab 时滞系统,深入探讨MATLAB中时滞系统的建模与仿真

深入探讨MATLAB中时滞系统的建模与仿真

在许多实际工程和科学问题中，时滞系统是一个常见的现象。时滞系统指的是系统输出或状态的变化受到过去输入或状态的影响。本文将详细介绍如何在MATLAB中建立时滞系统的模型，并进行仿真分析。

一、时滞系统的基本概念

时滞系统是指系统在某一时刻的输出或状态不仅取决于当前时刻的输入或状态，还受到过去时刻输入或状态的影响。时滞系统在许多领域都有应用，如控制理论、信号处理、生物医学等。

二、MATLAB中时滞系统的建模

在MATLAB中，我们可以使用传递函数、状态空间模型或差分方程来描述时滞系统。

2.1 传递函数模型

传递函数模型是时滞系统最常用的建模方法之一。对于一阶时滞系统，其传递函数可以表示为：

$$G(s) = frac{K}{s + tau}$$

其中，$K$为系统增益，$tau$为时滞。

2.2 状态空间模型

状态空间模型是另一种常用的建模方法。对于一阶时滞系统，其状态空间模型可以表示为：

$$begin{cases}

dot{x}(t) = A x(t) + B u(t) + C e(t)

y(t) = D x(t) + E u(t) + F e(t)

end{cases}$$

其中，$x(t)$为状态向量，$u(t)$为输入向量，$y(t)$为输出向量，$e(t)$为时滞项。

2.3 差分方程模型

差分方程模型是另一种描述时滞系统的方法。对于一阶时滞系统，其差分方程可以表示为：

$$y(t) = A y(t - tau) + B u(t) + C e(t)$$

其中，$A$、$B$、$C$为系统参数，$tau$为时滞。

三、MATLAB中时滞系统的仿真

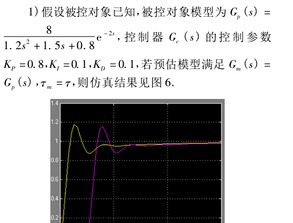
在MATLAB中，我们可以使用Simulink工具箱对时滞系统进行仿真分析。

3.1 Simulink建模

在Simulink中，我们可以通过以下步骤建立时滞系统的模型：

打开Simulink库浏览器，选择相应的模块，如传递函数、状态空间或差分方程模块。

将模块拖拽到Simulink编辑窗口中，并连接模块以形成系统模型。

设置模块参数，如系统增益、时滞等。

3.2 仿真分析

在Simulink中，我们可以通过以下步骤对时滞系统进行仿真分析：

在Simulink编辑窗口中，选择“仿真”菜单下的“开始仿真”选项。

观察仿真结果，如系统输出、状态变量等。

分析仿真结果，如稳定性、性能等。

四、结论

本文介绍了在MATLAB中建立时滞系统模型并进行仿真分析的方法。通过传递函数、状态空间或差分方程模型，我们可以描述时滞系统的动态特性。利用Simulink工具箱，我们可以方便地对时滞系统进行仿真分析，从而更好地理解系统的行为。