matlab 离散时间系统,MATLAB在离散时间系统中的应用与实现

MATLAB在离散时间系统中的应用与实现

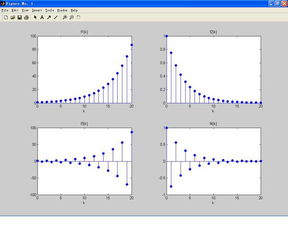
随着计算机技术的飞速发展，MATLAB作为一种高性能的数学计算软件，在各个领域得到了广泛的应用。在信号与系统领域，离散时间系统是研究的重要内容之一。本文将介绍MATLAB在离散时间系统中的应用与实现，帮助读者更好地理解和掌握这一领域。

一、离散时间系统的基本概念

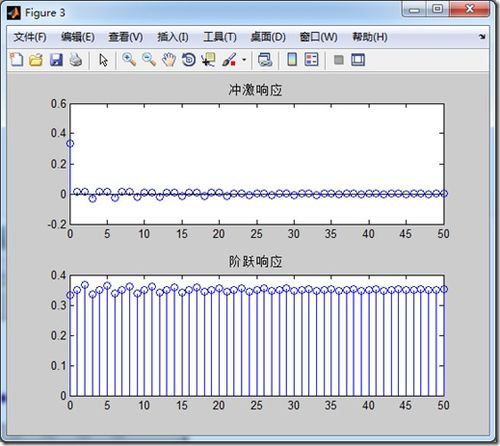
离散时间系统是指系统中的信号和参数都是离散的，即信号和参数只在特定的时刻存在。离散时间系统在数字信号处理、通信系统、控制理论等领域有着广泛的应用。离散时间系统的基本数学模型包括差分方程、Z变换、离散傅里叶变换等。

二、MATLAB在离散时间系统建模中的应用

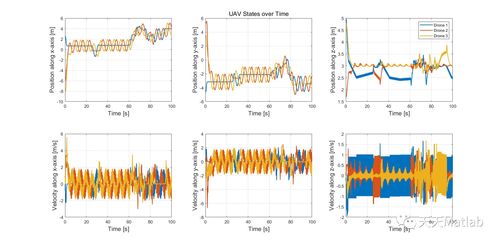
1. 差分方程建模

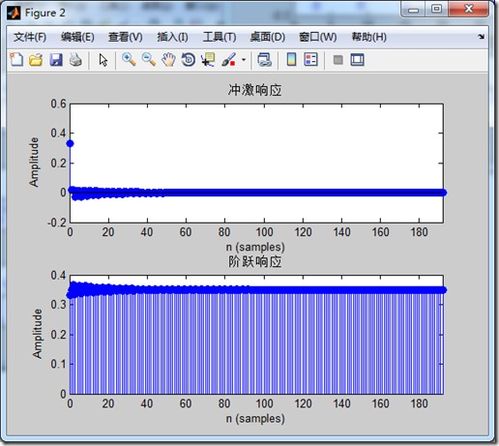
差分方程是描述离散时间系统动态特性的基本数学工具。在MATLAB中，可以使用`diff`函数对离散时间信号进行求导，从而得到差分方程。例如，对于一个一阶离散时间系统，其差分方程可以表示为：

y[n] = a1 y[n-1] + b1 x[n]

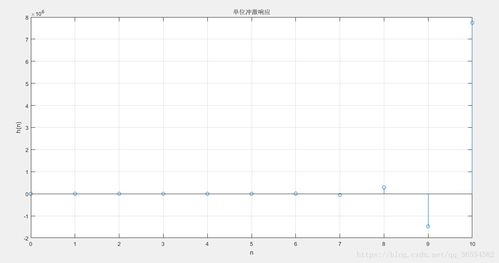
2. Z变换建模

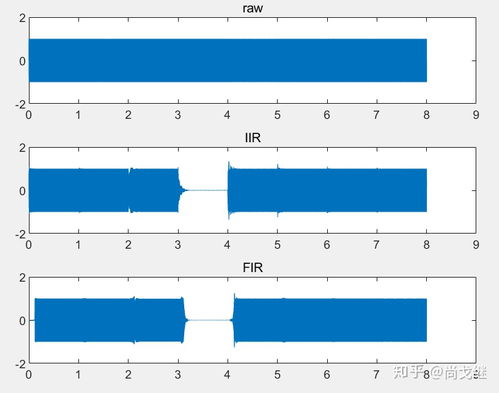
Z变换是离散时间系统的一个重要数学工具，可以将离散时间信号从时域转换到Z域。在MATLAB中，可以使用`ztrans`函数对离散时间信号进行Z变换。例如，对于一个一阶离散时间系统，其Z变换可以表示为：

H(z) = 1 / (1 - a1 z^-1)

3. 离散傅里叶变换建模

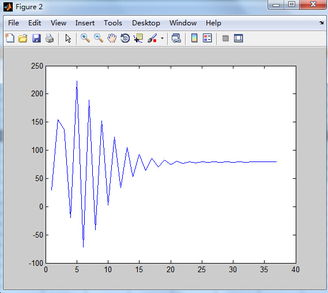
离散傅里叶变换（DFT）是离散时间系统频域分析的重要工具。在MATLAB中，可以使用`fft`函数对离散时间信号进行DFT。例如，对于一个离散时间信号，其DFT可以表示为：

X[k] = Σ(x[n] e^(-j 2 π k n / N))

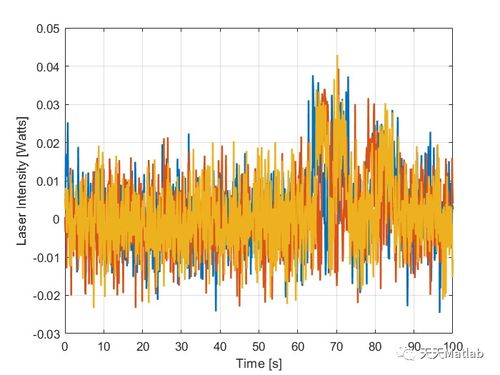
三、MATLAB在离散时间系统分析中的应用

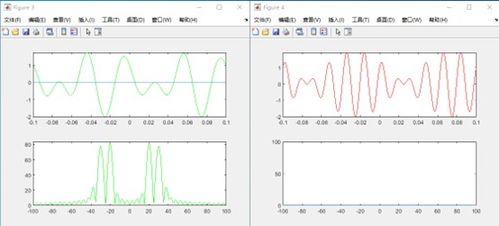
在MATLAB中，可以对离散时间系统进行多种分析，包括稳定性分析、时域分析、频域分析等。

1. 稳定性分析

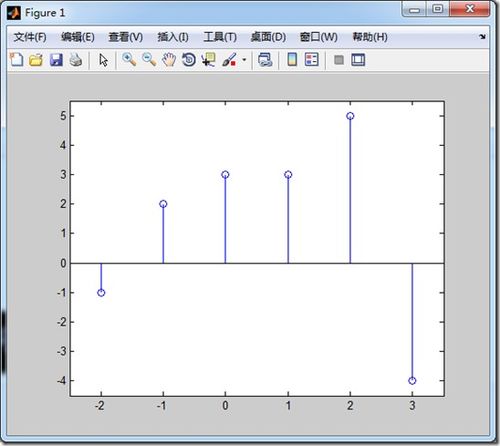
稳定性分析是评估离散时间系统性能的重要指标。在MATLAB中，可以使用`roots`函数计算系统的极点，从而判断系统的稳定性。例如，对于一个一阶离散时间系统，其极点可以表示为：

ρ = a1

如果ρ的绝对值小于1，则系统是稳定的。

2. 时域分析

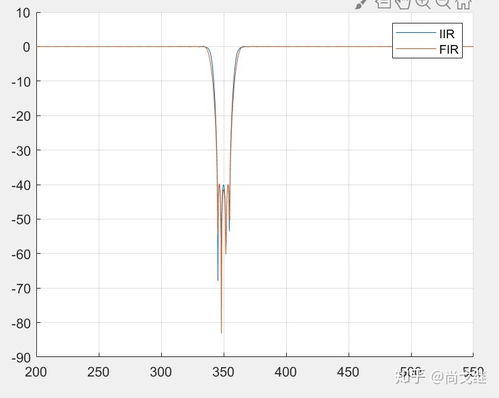
时域分析是研究离散时间系统在时域内的动态特性。在MATLAB中，可以使用`lsim`函数对离散时间系统进行时域分析。例如，对于一个一阶离散时间系统，其时域响应可以表示为：

y[n] = a1^n x[n]

3. 频域分析

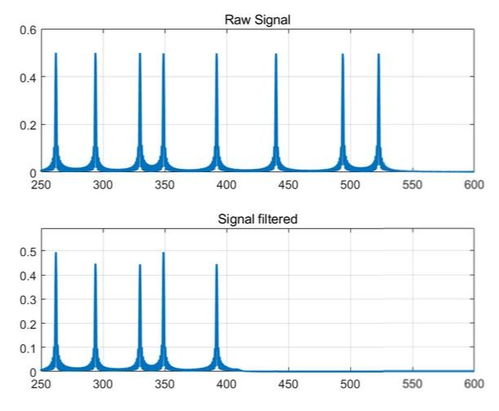
频域分析是研究离散时间系统在频域内的动态特性。在MATLAB中，可以使用`freqz`函数对离散时间系统进行频域分析。例如，对于一个一阶离散时间系统，其频域响应可以表示为：

H(e^(j ω)) = 1 / (1 - a1 e^(-j ω))