pc公理系统,逻辑推理的基石

PC公理系统：逻辑推理的基石

在数学和逻辑学领域，公理系统是一种基础的理论框架，它通过一组公理和推导规则来构建整个理论体系。PC公理系统，全称为命题演算公理系统，是数理逻辑中的一个重要分支，它为我们提供了对命题逻辑进行形式化推理的工具。

一、PC公理系统的起源与发展

PC公理系统起源于19世纪末，由德国数学家弗雷格（Gottlob Frege）和英国数学家罗素（Bertrand Russell）等人提出。他们试图通过形式化的方法来研究数学的基础，从而避免数学中的悖论和矛盾。PC公理系统的发展经历了多个阶段，逐渐形成了今天我们所熟知的形态。

二、PC公理系统的基本概念

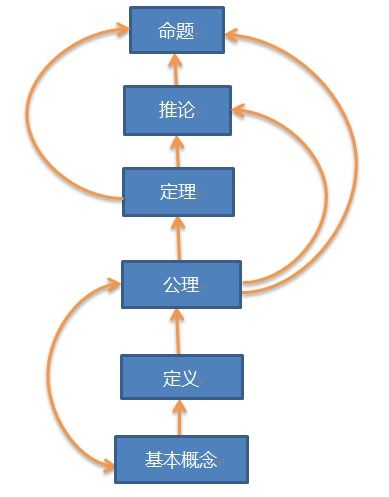
PC公理系统由一组公理和推导规则组成。公理是无需证明的基本命题，它们构成了整个系统的基石。在PC公理系统中，主要有以下几种公理：

公理1：如果A为真，则A为真。

公理2：如果A为真，则A或B为真。

公理3：如果A为真，且A或B为真，则B为真。

这些公理通过逻辑运算符（如合取、析取、否定等）和量词（如全称量词、存在量词等）来表达。推导规则则用于从已知命题推导出新的命题。

三、PC公理系统的应用

数学证明：PC公理系统可以用于证明数学中的定理和公式。

程序验证：在计算机科学中，PC公理系统可以用于验证程序的正确性。

人工智能：在人工智能领域，PC公理系统可以用于构建知识表示和推理系统。

PC公理系统的应用不仅限于理论研究，它在实际应用中也发挥着重要作用。

四、PC公理系统的局限性

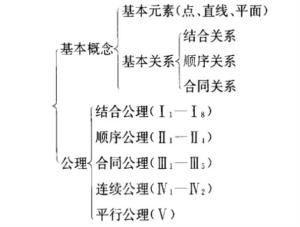
不完全性：PC公理系统不能证明所有有效的命题，这意味着存在一些真命题无法在PC公理系统中得到证明。

完备性：PC公理系统也不能证明所有无效的命题，这意味着存在一些假命题在PC公理系统中被错误地证明为真。

因此，在使用PC公理系统进行推理时，我们需要注意其局限性，并寻求其他方法来弥补这些不足。

PC公理系统是数理逻辑中的一个重要分支，它为我们提供了对命题逻辑进行形式化推理的工具。通过一组公理和推导规则，PC公理系统可以构建起一个完整的理论体系，并在数学、计算机科学、人工智能等领域得到广泛应用。PC公理系统也存在一些局限性，我们需要在应用中注意这些局限性，并寻求其他方法来弥补不足。