matlab 信号系统,信号表示

随着信息技术的飞速发展，信号处理技术在各个领域都得到了广泛应用。MATLAB作为一种功能强大的数学计算软件，在信号系统分析、设计、仿真等方面具有显著优势。本文将介绍MATLAB在信号系统领域的应用，包括信号表示、变换、滤波、调制解调等，旨在为读者提供MATLAB信号系统分析的基本方法和技巧。

信号表示

向量表示：向量可以表示离散时间信号，其中每个元素代表信号在某个时间点的值。

矩阵表示：矩阵可以表示连续时间信号，其中每一列代表信号在某个时间点的值。

函数表示：函数可以表示连续时间信号，通过定义函数表达式来描述信号随时间的变化。

信号变换

傅里叶变换：傅里叶变换可以将信号从时域转换为频域，便于分析信号的频率成分。

拉普拉斯变换：拉普拉斯变换可以将信号从时域转换为复频域，适用于分析线性时不变系统。

Z变换：Z变换可以将信号从时域转换为Z域，适用于分析离散时间系统。

信号滤波

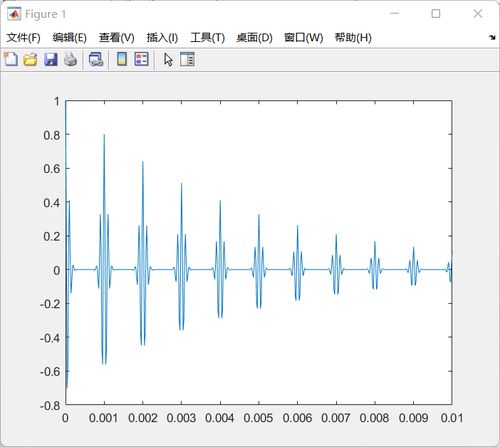
低通滤波器：低通滤波器允许低频信号通过，抑制高频信号。

高通滤波器：高通滤波器允许高频信号通过，抑制低频信号。

带通滤波器：带通滤波器允许特定频率范围内的信号通过，抑制其他频率信号。

带阻滤波器：带阻滤波器抑制特定频率范围内的信号，允许其他频率信号通过。

信号调制解调

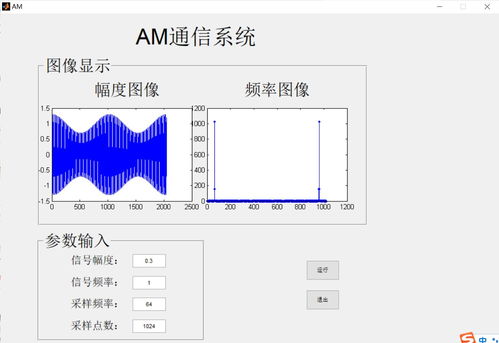
幅度调制：幅度调制（AM）将信号与载波信号相乘，实现信号的传输。

频率调制：频率调制（FM）通过改变载波信号的频率来传输信号。

相位调制：相位调制（PM）通过改变载波信号的相位来传输信号。

MATLAB信号系统分析实例

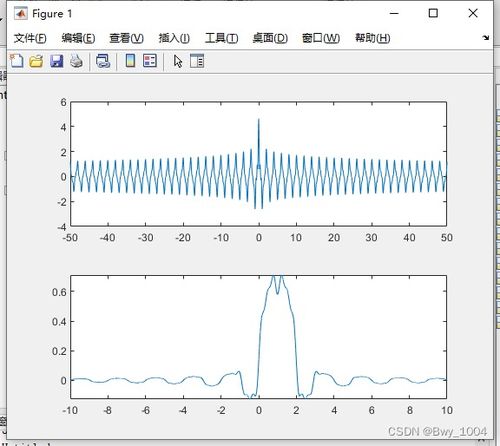
以下是一个使用MATLAB进行信号系统分析的实例，我们将分析一个简单的低通滤波器。

% 定义低通滤波器的截止频率

fc = 10; % Hz

% 定义采样频率

fs = 100; % Hz

% 定义滤波器阶数

N = 5;

% 设计低通滤波器

[b, a] = butter(N, fc/(fs/2), 'low');

% 生成测试信号

t = 0:1/fs:1-1/fs; % 生成时间向量

x = sin(2pi5t); % 生成正弦信号

% 滤波信号

y = filter(b, a, x);

% 绘制滤波前后的信号

subplot(2,1,1);

plot(t, x);

title('滤波前的信号');

subplot(2,1,2);

plot(t, y);

title('滤波后的信号');

本文介绍了MATLAB在信号系统领域的应用，包括信号表示、变换、滤波、调制解调等。通过MATLAB，我们可以方便地进行信号系统分析、设计和仿真，为实际工程应用提供有力支持。