matlab求系统响应,MATLAB在系统响应分析中的应用

MATLAB在系统响应分析中的应用

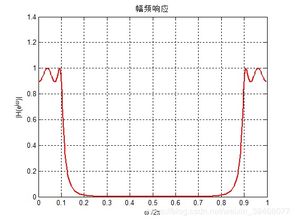
随着科学技术的不断发展，系统响应分析在工程、物理、生物等多个领域都扮演着重要的角色。MATLAB作为一种功能强大的数学计算软件，在系统响应分析中具有广泛的应用。本文将介绍MATLAB在系统响应分析中的应用，包括系统响应的求解方法、实例分析以及MATLAB工具箱的使用。

一、系统响应的求解方法

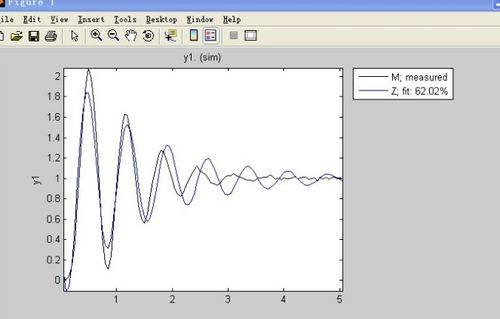
系统响应是指系统在受到外部激励后，输出信号随时间的变化过程。根据系统类型的不同，系统响应可以分为以下几种：

零状态响应：系统初始状态为零时，受到外部激励后的响应。

零输入响应：系统外部激励为零时，系统内部状态变化引起的响应。

完全响应：系统初始状态和外部激励共同作用下的响应。

在MATLAB中，我们可以通过以下方法求解系统响应：

拉普拉斯变换法：将微分方程转化为代数方程，求解代数方程后，再进行拉普拉斯逆变换得到系统响应。

数值解法：利用MATLAB内置函数，如`ode45`、`ode23`等，对微分方程进行数值求解。

系统函数法：利用MATLAB内置函数，如`lsim`、`step`等，根据系统函数求解系统响应。

二、实例分析

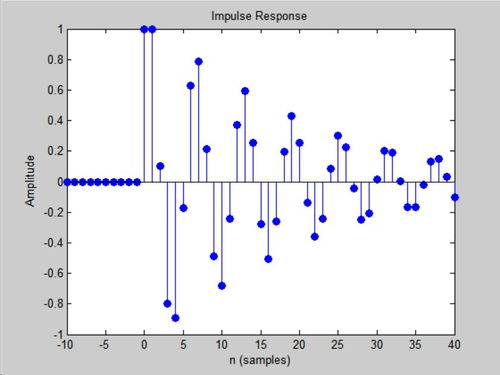
以下是一个简单的实例，说明如何使用MATLAB求解系统响应。

假设一个系统的微分方程为：y'' + 2y' + y = x(t)，其中x(t)为单位阶跃信号。

1. 拉普拉斯变换法：

syms y(t) x(t);

ode = diff(y, t, 2) + 2diff(y, t) + y - x(t);

s = laplace(ode, y, t);

y_inv = ilaplace(s, y, t);

2. 数值解法：

syms y(t);

tspan = [0, 10];

ic = [y(0), 0];

[t, y] = ode45(@(t, y) diff(y, t, 2) + 2diff(y, t) + y - x(t), tspan, ic);

3. 系统函数法：

sys = tf([1, 2, 1], [1, 2, 1]);

step(sys);

三、MATLAB工具箱的使用

在MATLAB中，有许多工具箱可以帮助我们进行系统响应分析，以下列举几个常用的工具箱：

Control System Toolbox：提供控制系统设计、分析和仿真功能。

Signal Processing Toolbox：提供信号处理和分析功能。

Simulink：提供动态系统建模、仿真和实时测试功能。

这些工具箱可以帮助我们方便地进行系统响应分析，提高工作效率。

本文介绍了MATLAB在系统响应分析中的应用，包括系统响应的求解方法、实例分析以及MATLAB工具箱的使用。通过本文的介绍，读者可以了解到MATLAB在系统响应分析中的强大功能，为实际工程应用提供参考。