matlab 求系统零极点,准备环境

在信号与系统领域，系统的零极点分析是理解系统动态行为和性能的关键。MATLAB作为一种强大的数学计算软件，提供了丰富的工具和函数来帮助我们求解系统的零极点。本文将详细介绍如何在MATLAB中求解系统的零极点，包括传递函数和离散时间系统。

准备环境

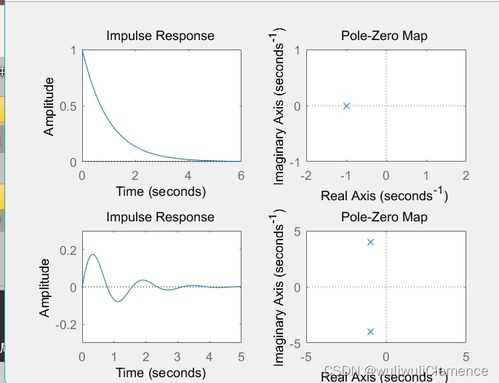
在开始之前，请确保您的计算机上已安装MATLAB软件。此外，您还需要安装Control System Toolbox，该工具箱提供了用于控制系统分析和设计的工具。

传递函数的零极点求解

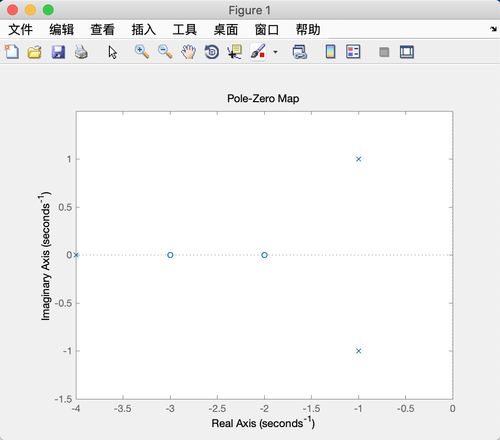
传递函数是描述线性时不变系统动态特性的数学模型。在MATLAB中，我们可以使用`tf`函数创建传递函数模型，并使用`zpk`函数求解其零极点。

```matlab

% 创建传递函数模型

num = [1 2]; % 分子系数

den = [1 3 2]; % 分母系数

G = tf(num, den);

% 求解零极点

[z, p, k] = zpk(G);

在上面的代码中，`num`和`den`分别代表传递函数的分子和分母系数。`tf`函数创建了一个传递函数模型`G`，然后`zpk`函数返回了系统的零点`z`、极点`p`和增益`k`。

离散时间系统的零极点求解

离散时间系统是信号与系统领域的重要组成部分。在MATLAB中，我们可以使用`zpk`函数直接求解离散时间系统的零极点。

```matlab

% 创建离散时间系统模型

num = [1 2]; % 分子系数

den = [1 3 2]; % 分母系数

G = tf(num, den, 'z');

% 求解零极点

[z, p, k] = zpk(G);

在上面的代码中，`tf`函数创建了一个离散时间系统模型`G`，其中`'z'`参数指定了系统是离散时间系统。然后`zpk`函数返回了系统的零点`z`、极点`p`和增益`k`。

绘制零极点图

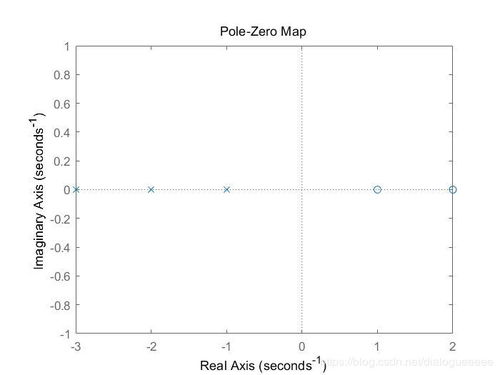
在MATLAB中，我们可以使用`zplane`函数绘制系统的零极点图，直观地展示零极点的分布情况。

```matlab

% 绘制传递函数的零极点图

zplane(G);

% 绘制离散时间系统的零极点图

zplane(G, 'z');

在上面的代码中，`zplane`函数分别绘制了传递函数和离散时间系统的零极点图。对于离散时间系统，需要指定`'z'`参数。

系统稳定性分析

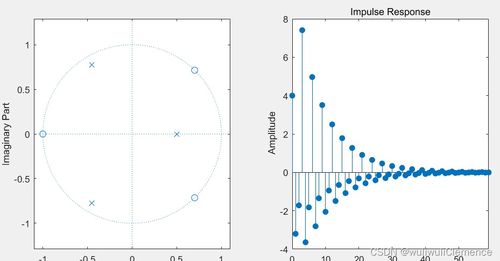
系统稳定性是控制系统设计中的一个重要指标。在MATLAB中，我们可以使用`isstable`函数判断系统是否稳定。

```matlab

% 判断传递函数是否稳定

isStable = isstable(G);

% 判断离散时间系统是否稳定

isStable = isstable(G, 'z');

在上面的代码中，`isstable`函数分别判断了传递函数和离散时间系统的稳定性。如果系统稳定，函数返回`true`，否则返回`false`。

本文介绍了如何在MATLAB中求解系统的零极点，包括传递函数和离散时间系统。通过使用`tf`、`zpk`、`zplane`和`isstable`等函数，我们可以方便地分析系统的动态特性和稳定性。这些工具和函数在信号与系统领域的研究和应用中具有重要意义。