tsp系统,什么是TSP系统？

什么是TSP系统？

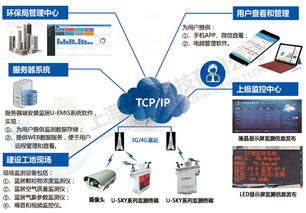
旅行商问题（Traveling Salesman Problem，简称TSP）是一个经典的组合优化问题，它要求在给定的城市集合中，寻找一条最短的路径，使得旅行商能够访问每个城市一次并返回起点。TSP系统则是为了解决这一问题而设计的一系列算法和软件工具。

TSP系统的应用领域

物流配送：优化配送路线，减少运输成本和时间。

城市规划：设计高效的公交线路或道路网络。

军事行动：规划物资运输路线，提高作战效率。

旅游规划：设计最佳旅游路线，提高游客体验。

TSP系统的算法原理

TSP系统通常采用以下几种算法来解决旅行商问题：

精确算法：如动态规划、分支限界法等，能够找到最优解，但计算复杂度高，不适用于大规模问题。

启发式算法：如遗传算法、模拟退火、蚁群算法等，能够在合理的时间内找到近似最优解，适用于大规模问题。

元启发式算法：如可变邻域搜索（VNS）、禁忌搜索（TS）等，通过改变搜索空间和邻域结构来跳出局部最优，寻找全局最优解。

TSP系统的实现方法

TSP系统的实现方法主要包括以下步骤：

数据输入：收集城市坐标、距离等信息。

算法选择：根据问题规模和需求选择合适的算法。

算法实现：编写算法代码，实现算法功能。

结果输出：输出最优路径、距离等信息。

系统优化：根据实际应用需求，对系统进行优化和调整。

TSP系统的优势与挑战

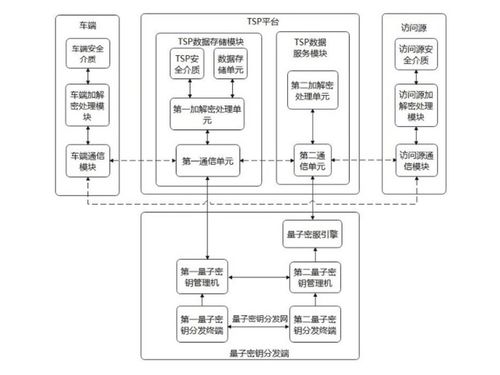
TSP系统具有以下优势：

提高效率：优化路径，减少时间和成本。

降低风险：避免重复路线，减少资源浪费。

提升用户体验：设计合理的路线，提高满意度。

然而，TSP系统也面临以下挑战：

计算复杂度高：大规模问题难以在合理时间内找到最优解。

数据质量：城市坐标、距离等信息的准确性影响算法效果。

算法选择：不同问题规模和需求需要选择合适的算法。

TSP系统作为一种解决旅行商问题的有效工具，在多个领域具有广泛的应用。随着算法和技术的不断发展，TSP系统将更加高效、智能，为各行各业带来更多价值。