svd推荐系统,原理、应用与优化

深入解析SVD推荐系统：原理、应用与优化

一、SVD推荐系统原理

SVD推荐系统，即奇异值分解推荐系统，是一种基于矩阵分解的推荐算法。它通过将用户-物品评分矩阵分解为三个矩阵，即用户特征矩阵U、奇异值矩阵S和物品特征矩阵V，从而实现推荐效果。

1. 用户-物品评分矩阵

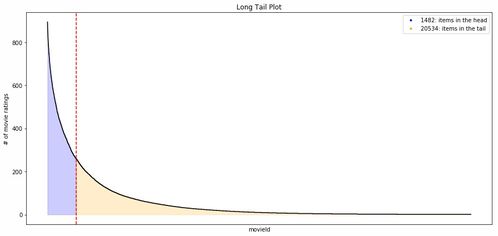
用户-物品评分矩阵是一个二维矩阵，其中行代表用户，列代表物品，矩阵中的元素表示用户对物品的评分。由于用户和物品的数量庞大，评分矩阵往往非常稀疏。

2. SVD分解

SVD分解是将用户-物品评分矩阵分解为三个矩阵的过程。具体步骤如下：

计算用户-物品评分矩阵的协方差矩阵。

对协方差矩阵进行特征值分解，得到特征值和特征向量。

对特征值进行排序，并获取对应的特征向量。

将特征值和特征向量组合，得到奇异值矩阵S和特征向量矩阵V。

将特征向量矩阵V的列向量进行正交化，得到用户特征矩阵U。

3. 推荐预测

通过SVD分解得到的用户特征矩阵U、奇异值矩阵S和物品特征矩阵V，可以预测用户对未评分物品的评分。具体步骤如下：

计算用户特征向量与物品特征向量的内积。

将内积与对应的奇异值相乘，得到预测评分。

二、SVD推荐系统应用

SVD推荐系统在多个领域都有广泛的应用，以下列举几个典型应用场景：

1. 电子商务

在电子商务领域，SVD推荐系统可以用于推荐商品、促销活动等，提高用户购买转化率和销售额。

2. 社交媒体

在社交媒体领域，SVD推荐系统可以用于推荐好友、兴趣小组等，增强用户社交体验。

3. 在线视频

在线视频平台可以利用SVD推荐系统为用户推荐电影、电视剧等，提高用户观看时长和平台活跃度。

三、SVD推荐系统优化

1. 缺失值处理

由于用户-物品评分矩阵的稀疏性，SVD分解过程中可能会出现缺失值。可以通过以下方法处理缺失值：

均值填充：用用户或物品的平均评分填充缺失值。

KNN填充：根据用户或物品的相似度，从邻居中获取评分填充缺失值。

2. 特征选择

在SVD分解过程中，可以通过选择重要的特征向量来提高推荐效果。可以通过以下方法进行特征选择：

基于特征值：选择特征值较大的特征向量。

基于相关性：选择与目标变量相关性较高的特征向量。

3. 优化算法

SVD分解的计算复杂度较高，可以通过以下方法优化算法：

并行计算：利用多核处理器并行计算SVD分解。

近似算法：使用近似算法降低计算复杂度。

SVD推荐系统作为一种基于矩阵分解的推荐算法，具有高效性和准确性。本文深入解析了SVD推荐系统的原理、应用与优化策略，为相关领域的研究和应用提供了参考。