matlab求系统函数,MATLAB中系统函数的求解与应用

MATLAB中系统函数的求解与应用

在信号与系统领域，系统函数是描述线性时不变系统的重要工具。它能够帮助我们分析系统的时域和频域特性。本文将介绍如何在MATLAB中求解系统函数，并探讨其在实际应用中的重要性。

一、系统函数的基本概念

系统函数H(z)是系统输入信号的Z变换与输出信号的Z变换之比。对于离散时间系统，系统函数可以表示为：

[ H(z) = frac{B(z)}{A(z)} ]

其中，B(z)和A(z)分别是系统函数的分子和分母多项式，z是复变量。

二、MATLAB中求解系统函数

1. `roots` 函数：用于求解多项式的根，即系统函数的零点。

```matlab

z = roots(b);

```

其中，`b` 是系统函数的分子多项式系数向量。

2. `poly` 函数：用于创建多项式系数向量。

```matlab

b = poly(roots(z));

```

其中，`z` 是系统函数的零点。

3. `freqz` 函数：用于计算离散时间系统的频率响应。

```matlab

[h, w] = freqz(b, a, N);

```

其中，`a` 是系统函数的分母多项式系数向量，`N` 是频率点数。

4. `zplane` 函数：用于绘制系统函数的零极点图。

```matlab

zplane(b, a);

```

其中，`b` 和 `a` 分别是系统函数的分子和分母多项式系数向量。

三、系统函数的应用

1. 系统稳定性分析：通过求解系统函数的极点，可以判断系统的稳定性。

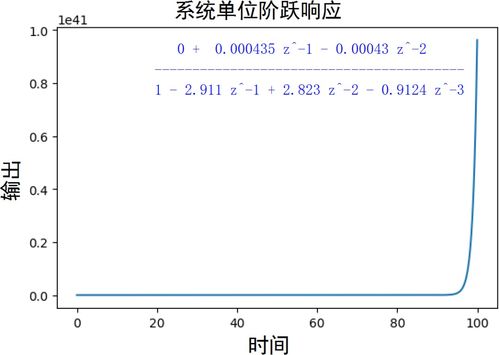
2. 系统时域响应分析：利用系统函数，可以计算系统的单位脉冲响应和单位阶跃响应。

3. 系统频域响应分析：通过计算系统函数的频率响应，可以分析系统的幅频特性和相频特性。

4. 系统设计：在系统设计过程中，可以利用系统函数来优化系统的性能。

四、MATLAB示例

以下是一个使用MATLAB求解系统函数的示例：

```matlab

% 定义系统函数的分子和分母多项式系数

b = [0.8, -0.44, 0.36, 0.02];

a = [1, 0.7, -0.45, -0.3];

% 求解系统函数的零点

z = roots(b);

% 创建系统函数的分子多项式系数

b = poly(z);

% 绘制系统函数的零极点图

zplane(b, a);

% 计算系统函数的频率响应

[h, w] = freqz(b, a, 512);

% 绘制系统函数的幅频特性

plot(w/pi, abs(h));

xlabel('omega/pi');

ylabel('幅度');

title('系统函数的幅频特性');

通过以上示例，我们可以看到MATLAB在求解系统函数方面的强大功能。

本文介绍了MATLAB中系统函数的求解方法及其应用。通过使用MATLAB提供的函数，我们可以方便地分析系统函数的时域和频域特性，为信号与系统领域的研究和应用提供有力支持。