matlab画系统响应,连续系统响应的绘制

在信号与系统领域，系统响应是描述系统对输入信号处理能力的重要指标。MATLAB作为一种强大的数学计算软件，提供了丰富的工具和函数来绘制和分析系统响应。本文将详细介绍如何在MATLAB中绘制系统响应，包括连续系统和离散系统的响应，并探讨一些常用的绘图技巧。

连续系统响应的绘制

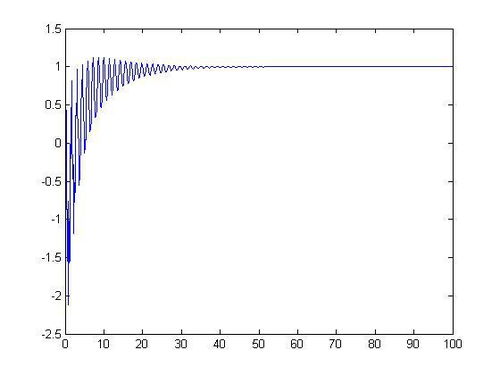
在MATLAB中，绘制连续系统响应通常涉及以下步骤：

定义输入信号：首先需要定义一个连续时间信号作为系统的输入。这可以通过编写MATLAB函数或使用内置信号函数实现。

定义系统模型：使用MATLAB的控制系统工具箱（Control System Toolbox）中的函数，如`tf`（传递函数）、`ss`（状态空间）等，定义系统的数学模型。

计算系统响应：使用`lsim`函数计算系统对输入信号的响应。该函数可以处理传递函数、状态空间模型和零点-极点-增益（ZPK）模型。

绘制响应：使用`plot`函数将系统响应绘制在图形窗口中。

以下是一个简单的示例，展示了如何绘制一个一阶系统的单位阶跃响应：

sys = tf([1], [1 1]); % 定义一阶系统

t = 0:0.01:5; % 定义时间向量

y = lsim(sys, 1, t); % 计算单位阶跃响应

plot(t, y);

xlabel('Time (s)');

ylabel('Response');

title('Unit Step Response of a First-Order System');

离散系统响应的绘制

定义输入信号：与连续系统相同，需要定义一个离散时间信号作为输入。

定义系统模型：使用`tf`、`ss`或`zpk`函数定义离散系统的数学模型。

计算系统响应：使用`lsim`函数计算离散系统对输入信号的响应。注意，`lsim`函数在处理离散系统时需要指定离散时间向量。

绘制响应：使用`plot`函数将系统响应绘制在图形窗口中。

以下是一个示例，展示了如何绘制一个离散系统的单位脉冲响应：

sys = tf([1], [1 -0.5]); % 定义离散系统

t = 0:0.01:5; % 定义时间向量

y = lsim(sys, [1 0], t); % 计算单位脉冲响应

plot(t, y);

xlabel('Time (s)');

ylabel('Response');

title('Unit Impulse Response of a Discrete System');

绘图技巧

在绘制系统响应时，以下技巧可以帮助您获得更清晰、更易于理解的图形：

调整坐标轴范围：使用`xlim`和`ylim`函数调整坐标轴的范围，以便更好地展示系统响应的关键特征。

添加网格：使用`grid on`命令在图形中添加网格，以便于观察系统响应的细节。

使用不同的线型：使用不同的线型（实线、虚线、点线等）来区分不同的系统响应曲线。

结论