matlab 控制系统 实例,基于MATLAB的控制系统实例分析

基于MATLAB的控制系统实例分析

随着科学技术的不断发展，控制系统在各个领域都发挥着至关重要的作用。MATLAB作为一种功能强大的科学计算软件，在控制系统设计、仿真和分析中具有广泛的应用。本文将结合一个具体的控制系统实例，介绍如何使用MATLAB进行控制系统的建模、仿真和分析。

控制系统是研究如何使系统输出满足预期目标的一门学科。在实际应用中，控制系统广泛应用于工业、交通、航空航天、生物医学等领域。MATLAB作为一种高性能的数学计算软件，具有强大的数值计算、符号计算和图形显示功能，为控制系统的研究提供了便利。

二、实例介绍

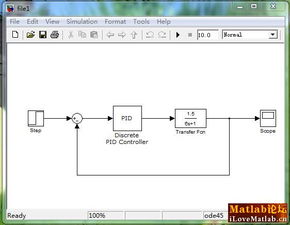
本文以一个简单的单输入单输出（SISO）控制系统为例，介绍如何使用MATLAB进行控制系统的建模、仿真和分析。该控制系统由一个比例-积分-微分（PID）控制器和一个被控对象组成。

三、控制系统建模

首先，我们需要对被控对象进行建模。在本例中，被控对象是一个一阶系统，其传递函数为G(s) = K/(s + T)，其中K为放大系数，T为时间常数。

```matlab

% 被控对象参数

K = 1;

T = 1;

% 建立传递函数模型

G = tf(K, [1 T]);

四、控制器设计

接下来，我们需要设计一个PID控制器。PID控制器由比例（P）、积分（I）和微分（D）三个部分组成，其传递函数为C(s) = Kp + Ki/s + Kds。在本例中，我们将采用MATLAB的PID Tuner工具箱进行控制器参数的自动整定。

```matlab

% 启动PID Tuner工具箱

pidtuner(G);

% 获取PID控制器参数

Kp = pidtuner.Kp;

Ki = pidtuner.Ki;

Kd = pidtuner.Kd;

五、系统仿真

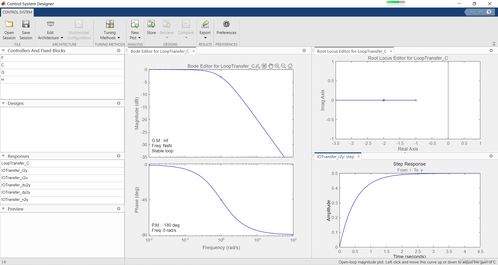
完成控制器设计后，我们可以使用MATLAB的Simulink模块进行系统仿真。Simulink是一个基于MATLAB的图形化仿真环境，可以方便地搭建控制系统模型并进行仿真。

```matlab

% 创建Simulink模型

% 运行仿真

六、结果分析

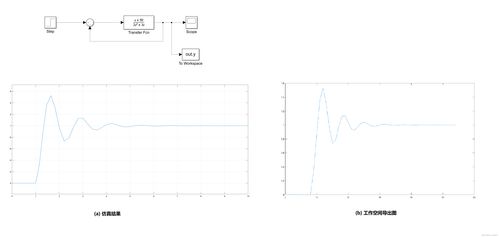
仿真完成后，我们可以通过观察系统的响应曲线来分析控制效果。在本例中，我们关注系统的稳态误差和超调量。通过调整PID控制器参数，我们可以得到满意的控制效果。

```matlab

% 获取系统响应曲线

t = 0:0.01:10;

y = lsim(GC, [1 0], t);

% 绘制系统响应曲线

plot(t, y);

xlabel('时间 (s)');

ylabel('输出');

title('系统响应曲线');

七、结论

本文通过一个简单的单输入单输出控制系统实例，介绍了如何使用MATLAB进行控制系统的建模、仿真和分析。MATLAB强大的功能为控制系统的研究提供了便利，有助于提高控制系统的设计质量和性能。