matlab求系统的阶跃响应曲线,准备系统模型

在自动控制系统中，阶跃响应是评估系统性能的重要指标之一。阶跃响应指的是系统在输入信号发生阶跃变化时的输出响应。MATLAB作为一种强大的数学计算软件，提供了丰富的工具和函数来分析和绘制系统的阶跃响应曲线。本文将详细介绍如何在MATLAB中求取系统的阶跃响应曲线，并分析其相关性能指标。

准备系统模型

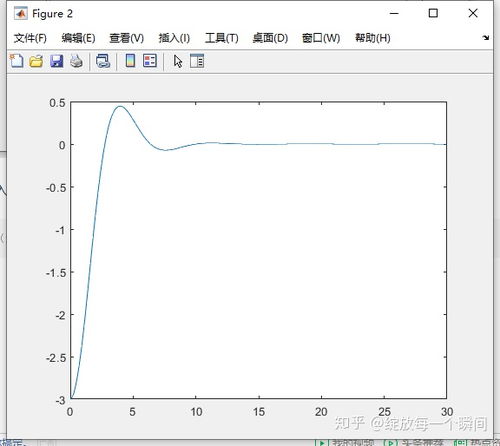
在进行阶跃响应分析之前，首先需要建立系统的数学模型。在MATLAB中，可以使用传递函数（Transfer Function）来描述线性时不变（LTI）系统。以下是一个简单的二阶系统传递函数的例子：

```matlab

num = [1 2]; % 分子多项式系数

den = [1 2 1]; % 分母多项式系数

sys = tf(num, den); % 创建传递函数模型

绘制阶跃响应曲线

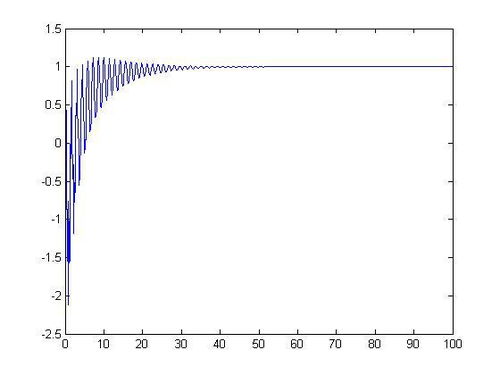
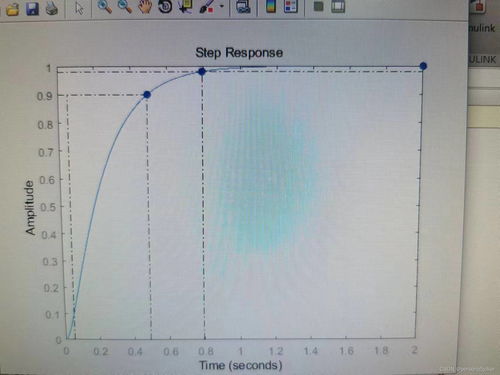
在MATLAB中，可以使用`step`函数来绘制系统的阶跃响应曲线。以下代码展示了如何绘制上述二阶系统的阶跃响应曲线：

```matlab

step(sys); % 绘制阶跃响应曲线

分析阶跃响应性能指标

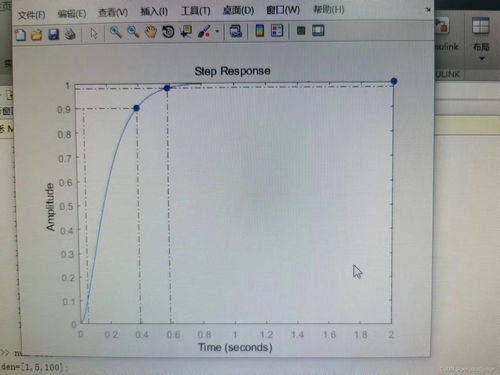
上升时间（rise time）：从阶跃响应的初始值到达到最终值（通常为100%）所需的时间。

峰值时间（peak time）：从阶跃响应的初始值到达到峰值所需的时间。

超调量（overshoot）：阶跃响应峰值与最终值之差与最终值的比值，通常以百分比表示。

调整时间（settling time）：从阶跃响应的初始值到达到最终值（通常为2%）所需的时间。

以下代码展示了如何计算上述性能指标：

```matlab

[y, t] = step(sys); % 获取阶跃响应曲线数据

rise_time = find(y >= 1, 1); % 计算上升时间

peak_time = find(y >= max(y), 1); % 计算峰值时间

overshoot = (max(y) - 1) / 1 100; % 计算超调量

使用Control System Toolbox进行更高级的分析

MATLAB的Control System Toolbox提供了更高级的系统分析功能，例如根轨迹、频率响应等。以下代码展示了如何使用Control System Toolbox绘制系统的根轨迹：

```matlab

rlocus(sys); % 绘制根轨迹

本文介绍了如何在MATLAB中求取系统的阶跃响应曲线，并分析了相关性能指标。通过使用MATLAB提供的工具和函数，可以方便地评估系统的动态性能，为控制系统设计提供依据。